Доверительный интервал для статистической дисперсии

Оценка (5) для дисперсии не является суммой независимых величин, так как в каждое слагаемое входит M^*X. Кроме того, она обладает заметной несимметрией. Все же при n>20 можно считать, что ее закон распределения близок к нормальному и использовать те же методы построения доверительного интервала. Для оценки (5) MD ^*X=s². Вывод формулы для дисперсии проводится сложно и мы приведем формулу без вывода:

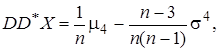
где m₄ - центральный момент 4-го порядка.

Для построения доверительного интервала нам нужно знать оценку момента 4-го порядка. Можно использовать оценку

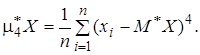
Однако при небольшом числе наблюдений погрешность оценки очень велика. Если других возможностей нет, то с этим приходится мириться. Часто закон распределения случайной величины известен заранее и, значит, известны теоретические оценки величины m₄. Тогда мы можем их использовать. Так для нормальной случайной величины m₄=3s⁴. Тогда

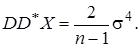(7)

Для равномерно распределенной на интервале [a;b] случайной величины X имеем

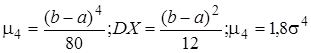
получим

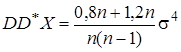
и т. д.

Если нет специальных оснований считать, что закон распределения сильно отличается от нормального, рекомендуется использовать формулу (7). Когда величина оценки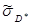выбрана, строим по заданной доверительной вероятности доверительный интервал для дисперсии по формуле

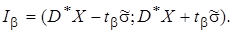
Пример.

В условиях предыдущего примера построить доверительный интервал для b=0,9. Тогда

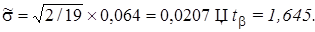
Доверительный интервал имеет вид

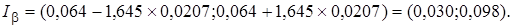
Дата добавления: 2014-01-07