Доверительный интервал для статистических оценок при точных законах распределения

Иногда удается построить точные законы распределения для оценок. Например, если случайная величина X нормально распределена, то случайная величина

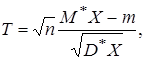
где M^*X задана формулой (1), а D^*X - формулой (5), распределена по закону Стьюдента с n степенями свободы.

В этом случае можно построить точный доверительный интервал для статистического математического ожидания. Запишем равенство (6) в виде

или

Получаем уравнение

2S(t_b)=b.

По заданному b и числу степеней свободы находим t_b. А затем определяем

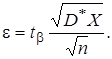
Доверительный интервал равен

Пример.

Дана таблица результатов наблюдений.

Построить доверительный интервал для b=0,9. Тогда M^*X=0,4 и D^*X=6,6. Для n-1=4, b=0,9 находим t_b=2,13.

Доверительный интервал равен

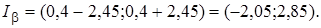
Для того же случая выборки из нормальной случайной величины случайная величина D^*X имеет вид

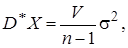(8)

где V распределена по закону c² с n-1 степенями свободы.

Закон распределения D^*X известен. Это позволяет построить доверительный интервал для дисперсии. Плотность распределения k_n-1(x) имеет асимметрию. Поэтому выберем интервал так, чтобы вероятность выхода за пределы доверительного интервала на правый участок равнялась вероятности попаданию на левый участок. Вероятность попадания на левый участок обозначим a/2=(1-b)/2. Тем самым мы однозначно выделили два значения c₁² и c₂², которые задают вероятности

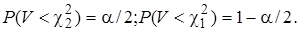
Получаем, что вероятность попадания V на интервал [c₂²;c₁²] равна

P(c₂²<V<c₁²)=b.

Интервал [c₂²;c₁²] является доверительным для величины V. Построим доверительный интервал для дисперсии, т. е. укажем такой интервал, чтобы

P(D₁<D<D₂)=b.

Из равенства (8) получаем

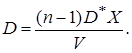
Поэтому неравенство c₂²<V соответствует неравенству

Аналогично неравенство V<c₁² соответствует неравенству

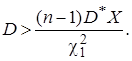
Доверительный интервал для дисперсии равен

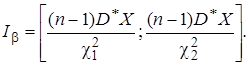
Пример.

В условиях нашего примера при условии, что распределено нормально, построить доверительный интервал для b=0,9. Тогда по таблице значений c² для n-1=19 находим

c₁²=30,1; c₂² =10,11.

Доверительный интервал имеет вид

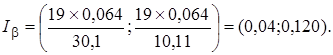
Дата добавления: 2014-01-07