
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способ. Метод Гаусса
|
|
|
|
Пример 1

1 шаг:

| 2 шаг:

|
3 шаг:

| 4 шаг:

|
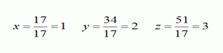
Ответ:

| Запишем расширенную матрицу этой системы уравнений, которая состоит из элементов уравнений данной матрицы. Наша задача: свести эту матрицу к ступенчатой, т.е. добиться того, чтобы в первой строке остались все четыре элемента, во второй строке - три, в третьей - два. Для обнуления элементов первого столбца работать будем с первой строкой, для обнуления элементов второго столбца - со второй строкой. Обнулять элементы третьего столбца нет необходимости. Исходную матрицу можно изменять, меняя местами строки. Работать лучше с матрицей у которой первый элемент строк и столбцов равен одному. Начнем приводить матрицу к ступенчатому виду. |

| 1 шаг: Обнулить элементы первого столбца второй и третьей строки. Для этого нам необходимо работать с первой строкой. В первой строке первого столбца стоит элемент 1. Найдем коэффициент, на который необходимо домножить эту единицу, чтобы при сложении с первым элементом второй строки в результате получился ноль. Т.е. необходимо определить на что надо домножить единицу, чтобы при сложении с числом 2 в результате получился ноль. Этим числом является (-2), т.к. 1*(-2)+2=0. Далее необходимо продолжить этот процесс до конца строки, т.е. каждый элемент первой строки домножить на (-2) и прибавить элемент второй строки: (-1)*(-2)+1=3 (второй столбец) и 2*(-2)+0=-4 (третий столбец) и 5*(-2)+4=-6 (четвертый столбец). |

| Теперь обнулим первый элемент третьей строки. Для этого нам необходимо опять работать с первой строкой. В первой строке первого столбца стоит элемент 1. Найдем коэффициент, на который необходимо домножить эту единицу, чтобы при сложении с первым элементом третьей строки в результате получился ноль. Т.е. необходимо определить на что надо домножить единицу, чтобы при сложении с числом 3 в результате получился ноль. Этим числом является (-3), т.к. 1*(-3)+3=0. Далее необходимо продолжить этот процесс до конца строки, т.е. каждый элемент первой строки домножить на (-3) и прибавить элемент третьей строки: (-1)*(-3)+5=8 (второй столбец) и 2*(-3)+1=-5 (третий столбец) и 5*(-3)+16=1 (четвертый столбец). |

| 2 шаг: Обнулить элемент второго столбца третьей строки. Для этого нам необходимо работать со второй строкой. Во второй строке первого столбца стоит элемент 0, его мы пропускаем и переходим ко второму столбцу. Там элемент равен 3. Найдем коэффициент, на который необходимо домножить эту тройку, чтобы при сложении со вторым элементом третьей строки в результате получился ноль. Т.е. необходимо определить на что надо домножить 3, чтобы при сложении с числом 5 в результате получился ноль. Этим числом является дробь (-8/3), т.к. 3*(-8/3)+8=0. Далее необходимо продолжить этот процесс до конца строки, т.е. каждый элемент первой строки домножить на (-8/3) и прибавить элемент третьей строки: -4 *(-8/3)-5=17/3 (третий столбец) и -6*(-8/3)+1=17 (четвертый столбец). Итак, мы свели матрицу к ступенчатому виду. |
3шаг: Запишем систему уравнений:
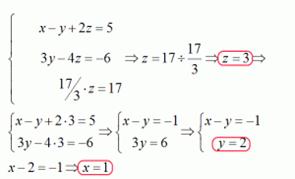
Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, например, для системы  матрица выглядит так:
матрица выглядит так:  .
.
Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае:  . Любую из матриц можно для краткости называть просто матрицей.
. Любую из матриц можно для краткости называть просто матрицей.
После того, как расширенная матрица система записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки: 
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу  . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них:
. В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них:  .
.
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить. Нулевая строка – это строка, в которой одни нули.
4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим, например, матрицу  . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2:
. Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2:
 .
.
Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля.
Рассмотрим нашу матрицу из практического примера:  . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2:
. Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: 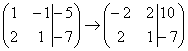 ,
,
и ко второй строке прибавляем первую строку умноженную на –2:  .
.
Теперь первую строку можно разделить «обратно» на –2: 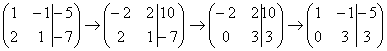 .
.
Как видно, строка, которую прибавляли – не изменилась. Всегда меняется строка, к которой прибавляют.
На практике так подробно, конечно, не расписывают, а пишут короче:
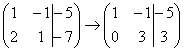 .
.
Еще раз: ко второй строке прибавили первую строку, умноженную на –2. Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:
«Переписываю матрицу и переписываю первую строку:  »
»
«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2:  , и ко второй строке прибавляю первую: 2 + (–2) = 0.
, и ко второй строке прибавляю первую: 2 + (–2) = 0.
Записываю результат во вторую строку: 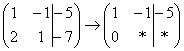 »
»
«Теперь второй столбец. Вверху –1 умножаю на –2:
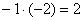 .
.
Ко второй строке прибавляю первую: 1 + 2 = 3.
Записываю результат во вторую строку:
 »
»
«И третий столбец. Вверху –5 умножаю на –2:
 .
.
Ко второй строке прибавляю первую: –7 + 10 = 3.
Записываю результат во вторую строку: 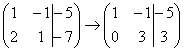 »
»
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 771; Нарушение авторских прав?; Мы поможем в написании вашей работы!