
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рекуррентные соотношения
|
|
|
|
Рекуррентным соотношением, рекуррентным уравнением или рекуррентной формулой называется соотношение вида  , которое позволяет вычислять все члены последовательности
, которое позволяет вычислять все члены последовательности 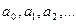 , если заданы ее первые k членов.
, если заданы ее первые k членов.
Пример 1.
1. Формула  задает арифметическую прогрессию.
задает арифметическую прогрессию.
2. Формула  определяет геометрическую прогрессию.
определяет геометрическую прогрессию.
3. Формула  задает последовательность чисел Фибоначчи.
задает последовательность чисел Фибоначчи.
В случае, когда рекуррентное соотношение линейно и однородно, т. е. выполняется соотношение вида
 (1)
(1)
(p =const), последовательность 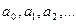 называется возвратной. Многочлен
называется возвратной. Многочлен
 (2)
(2)
называется характеристическим для возвратной последовательности  . Корни многочлена
. Корни многочлена  называются характеристическими.
называются характеристическими.
Множество всех последовательностей, удовлетворяющих данному рекуррентному соотношению, называется общим уравнением.
Описание общего уравнения соотношения (1) имеет аналоги с описанием решения обыкновенного дифференциального уравнения с постоянными коэффициентами.
Теорема 1. 1 .Пусть  - корень характеристического многочлена (2). Тогда последовательность
- корень характеристического многочлена (2). Тогда последовательность  , где c – произвольная константа, удовлетворяет соотношению (1).
, где c – произвольная константа, удовлетворяет соотношению (1).
2. Если  - простые корни характеристического многочлена (2), то общее решение рекуррентного соотношения (1) имеет вид
- простые корни характеристического многочлена (2), то общее решение рекуррентного соотношения (1) имеет вид  , где
, где  - произвольные константы.
- произвольные константы.
3. Если  - корень кратности
- корень кратности  характеристического многочлена (2), то общее решение рекуррентного соотношения (1) имеет вид
характеристического многочлена (2), то общее решение рекуррентного соотношения (1) имеет вид  , где
, где - произвольные константы.
- произвольные константы.
Зная общее решение рекуррентного уравнения (1), по начальным условиям,  можно найти неопределенные постоянные
можно найти неопределенные постоянные  и те самым получить решение уравнения (1) с данными начальными условиями.
и те самым получить решение уравнения (1) с данными начальными условиями.
Пример 2. Найти последовательность  , удовлетворяющую рекуррентному соотношению
, удовлетворяющую рекуррентному соотношению 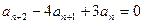 и начальным условиям
и начальным условиям  .
.
Корням характеристического многочлена  являются числа
являются числа  . Следовательно, по теореме 3.1. общее решение имеет вид
. Следовательно, по теореме 3.1. общее решение имеет вид  . Используя начальные условия, получаем систему
. Используя начальные условия, получаем систему
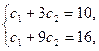
решая которую, находим  и
и  . Таким образом,
. Таким образом,  .
.
Рассмотрим неоднородное линейное рекуррентное уравнение
 (3)
(3)
Пусть  - общее решение однородного уравнения (1), а
- общее решение однородного уравнения (1), а  - частное (конкретное) решение неоднородного уравнения (3). Тогда последовательность
- частное (конкретное) решение неоднородного уравнения (3). Тогда последовательность  образует общее решение уравнения (3), и тем самым справедлива.
образует общее решение уравнения (3), и тем самым справедлива.
Теорема 2. Общее решение неоднородного линейного рекуррентного уравнения представляется в виде суммы общего решения соответствующего однородного линейного рекуррентного уравнения и некоторого частного решения неоднородного уравнения.
Таким образом, в силу теоремы 1. задача нахождения общего решения рекуррентного уравнения (3) сводится к нахождению некоторого частного решения.
В отдельных случаях имеются общие рецепты нахождения общего решения.
Если  (где
(где  ) не является характеристическим корнем, то, подставляя
) не является характеристическим корнем, то, подставляя  в (3), получаем
в (3), получаем  и отсюда
и отсюда  , т. е. частное решение можно задать формулой
, т. е. частное решение можно задать формулой  .
.
Пусть  - многочлен степени r от переменной n, и число 1 не является характеристическим корнем. Тогда и частное решение следует искать в виде
- многочлен степени r от переменной n, и число 1 не является характеристическим корнем. Тогда и частное решение следует искать в виде  . Подставляя многочлены в формулу (3), получаем
. Подставляя многочлены в формулу (3), получаем 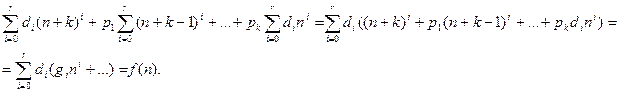
Сравнивая коэффициенты в левой и правой частях последнего равенства, получаем соотношения чисел  , позволяющие эти числа определить.
, позволяющие эти числа определить.
Пример. Найти решение уравнения
 (4)
(4)
с начальным условием  .
.
Рассмотрим характеристический многочлен  . Так как
. Так как  и правая часть
и правая часть  уравнения (3) равна n +1, то частное решение будем искать в виде
уравнения (3) равна n +1, то частное решение будем искать в виде  . Подставляя
. Подставляя  в уравнение (4), получаем
в уравнение (4), получаем  . Приравнивая коэффициенты в левой и правой частях последнего равенства, получаем систему
. Приравнивая коэффициенты в левой и правой частях последнего равенства, получаем систему
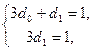
откуда находим  . Таким образом, частное решение уравнения (4) имеет вид
. Таким образом, частное решение уравнения (4) имеет вид  . По теореме 3.1. общее решение однородного уравнения
. По теореме 3.1. общее решение однородного уравнения  задается формулой
задается формулой  , и по теореме 3.2. получаем общее решение уравнения (4):
, и по теореме 3.2. получаем общее решение уравнения (4): 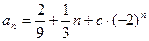 . Из начального условия
. Из начального условия  находим
находим  , т. е.
, т. е.  . Таким образом,
. Таким образом, 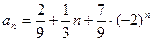 .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 3101; Нарушение авторских прав?; Мы поможем в написании вашей работы!