Проверка статистических гипотез о частоте

Постановка задачи проверки статистических гипотез

Проверка статистических гипотез

ТМ к лекции № 12

Специальные виды дисциплинарных взысканий.

Правила внутреннего трудового распорядка как основа трудовой дисциплины.

5. Изучить и законспектировать в рабочих тетрадях ст. 195 ТК РФ «Привлечение к дисциплинарной ответственности руководителя организации, руководителя структурного подразделения организации, их заместителей по требованию представительного органа работников».

Старший преподаватель кафедры

гражданско-правовых дисциплин

подполковник юстиции Э.В. Луговский

[1] Время определяется для каждого занятия в зависимости от наличия или отсутствия информирования на занятии

[2] Казанцев В.И. Трудовое право: учебник, 4-е изд. стер. М.: Издательский центр «Академия», 2008. – 432 с.

Каждый статистический ряд содержит как случайную составляющую, вызванную ограниченностью числа наблюдений и влиянием случайных факторов в момент проведения наблюдений, так и закономерную. Поэтому делать какие-то утверждения на основе этого ряда, вообще говоря, нельзя. Из-за случайного характера они могут оказаться, как верными, так и неверными. Мы можем лишь выдвигать гипотезы (предположения). И статистические данные могут находиться в согласии с гипотезой или противоречить ей. Большего добиться от статистического исследования мы не можем. Возникает задача проверки статистической гипотезы.

Для решения этой задачи задается доверительная вероятность b. Свяжем с данной гипотезой некоторый формализуемый признак. По данной доверительной вероятности b находим доверительный интервал для этого признака, связанного с исследуемой гипотезой. А затем по данному статистическому ряду вычислим величину этого признака для данного ряда. Если вычисленная величина признака выходит за допустимые пределы доверительного интервала, то гипотеза противоречит результатам наблюдений и ее следует отклонить. Если не выходит, то гипотеза согласуется с результатами наблюдений и ее следует принять. Таким образом, все, что можно утверждать на основе статистических наблюдений, - это данные противоречат или не противоречат гипотезе.

При этом возможны ошибки двух родов. Ошибка первого рода: мы отклоняем гипотезу, когда она выполняется. Ошибка второго рода: мы принимаем гипотезу, когда она не выполняется.

Вместо доверительной вероятности b часто используется уровень значимости a. Они связаны соотношением b=1-a. Обычно уровень значимости выражается в процентах.

Рассмотрим проверку гипотезы о частоте. Пусть вероятность появления события A в единичном испытании равна p. Проведено n=280 испытаний, число появлений m=151. Выдвигается гипотеза, что p=1/2. Согласуется ли гипотеза с данными опыта. В соответствии с гипотезой

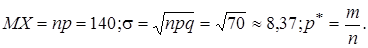
По интегральной теореме Муавра-Лапласа число появлений X события A имеет закон распределения, близкий к нормальному с параметрами a=MX=140 и s²=npq. Зададим доверительную вероятность b, например, b=0,95. Найдем по доверительной вероятности величину t_b из равенства

Или из равенства

Для b=0,95 величина t_b=1,96. Тогда доверительный интервал для числа появлений равен

I_b=(140-1,96×8,37; 140-1,96×8,37)=(123,6;156,4).

Мы видим, что значение m=151 попадает в доверительный интервал, данные не противоречат гипотезе и ее следует принять.

Дата добавления: 2014-01-07