Напряженность электростатического поля. Принцип суперпозиции электрических полей. Поток вектора

Электрические заряды, их свойства и классификация. Закон Кулона.

Электрический заряд - физическая величина, характеризующая интенсивность электромагнитного взаимодействия тел. Сам по себе электрический заряд не существует, его носителем может быть только частица вещества.

Основные свойства

1. Двойственность: в природе существуют заряды двух знаков, одноименные отталкиваются, разноименные притягиваются. В связи с этим заряды условного разделены на положительные и отрицательные.

Положительным назван заряд, которым обладает стеклянная палочка, потертая о шелк или бумагу.

Отрицательный - заряд, которым обладает янтарная или эбонитовая палочка, потертая о мех или шерсть.

2. Квантование: если физическая величина принимает только определенные дискретные значения, говорят, что она квантуется (дискретна). Опыт показывает, что любой электрический заряд квантуется, т.е. состоит из целого числа элементарных зарядов:

,

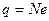где 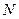=1,2,…целое число; e =1,6·1 ^-19Кл - элементарный заряд.

Наименьшим (элементарным) отрицательным зарядом обладает электрон, положительным - протон.

[q]=1Кл

1 кулон - заряд, проходящий через поперечное сечение проводника за одну секунду, когда по проводнику идет постоянный ток силой один ампер.

3. Сохранение заряда.

Электрические заряды могут исчезать и возникать вновь только парами. В каждой такой паре заряды равны по величине и противоположны по знаку. Например, электрон и позитрон при встрече аннигилируют, т.е. превращаются в нейтральные g- фотоны, при этом исчезают заряды –e и +e. В ходе процесса, называемого рождением пары, g - фотон, попадая в поле атомного ядра, превращается в пару частиц электрон и позитрон, при этом возникают заряды +e и –e.

Закон сохранения заряда: в изолированной системе алгебраическая сумма зарядов остается постоянной величиной при всех изменениях внутри системы.

Изолированной называется система тел, которая не обменивается зарядами с внешней средой.

4. Инвариантность заряда к различным инерциальным системам отсчета.

Опыт показывает, что величина заряда не зависит от скорости движения заряженного тела. Один и тот же заряд, измеренный в разных инерциальных системах отчета, одинаков.

5. Аддитивность: .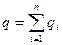

Классификация зарядов.

В зависимости от размеров заряженного тела заряды делят на точечные и протяженные.

· Точечными зарядом называют заряженное тело, размерами которого можно пренебречь в условиях данной задачи.

· Протяженным называется заряд тела, размерами которого в условиях данной задачи пренебречь нельзя. Протяженные заряды делятся на линейные, поверхностные и объемные.

По способности смещаться относительно положения равновесия под действием внешнего эл. поля заряды условно делят на свободные, связанные и сторонние.

Свободными называют заряды, способные свободно перемещаться в теле под действием внешнего эл. поля.

Связанными называют заряды, входящие в состав молекул диэлектриков, которые под действие эл. поля могут лишь смещаться из своего положения равновесия, но покинуть молекулу не могут.

Сторонними называются заряды, находящиеся на диэлектрике, но не входящие в состав его молекул.

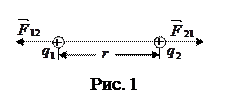Закон, которому подчиняется сила взаимодействия точечных зарядов (рис. 1), был установлен экспериментально в 1785г. Кулоном.

.

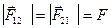Закон Кулона: сила взаимодействия двух неподвижных точечных зарядов прямо пропорциональна зарядам, обратно пропорциональна квадрату расстояния между ними, направлена вдоль прямой, соединяющей заряды, и зависит от среды, в которой они находятся.

,

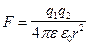где q_1,q₂- величины зарядов; r - расстояние между зарядами;

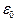=8,85·1 ^-12 Кл²/(Н·м²) - электрическая постоянная;

e - диэлектрическая проницаемость среды.

диэлектрическая проницаемость вещества показывает, во сколько раз сила взаимодействия зарядов в данном диэлектрике меньше, чем в вакууме, 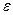_{вакуума}=1, 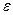- безразмерная величина.

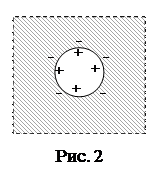Объясним причину этого ослабления, для чего рассмотрим заряженный шарик, окруженный диэлектриком (рис. 2). Поле шарика ориентирует молекулы диэлектрика, и на поверхности диэлектрика, примыкающей к шарику, появляются отрицательные связанные заряды.

Поле в любой точке диэлектрика будут создавать две противоположно заряженные сферы: поверхность шарика, заряженная положительно, и примыкающая к ней отрицательно заряженная поверхность диэлектрика, при этом из поля свободных зарядов вычитается поле связанных зарядов, и суммарное поле будет более слабым, чем поле одного шара.

Всякий заряд изменяет свойства окружающего пространства - создает в нем электрическое поле.

Электрическое поле - одна из форм существования материи, окружающей электрические заряды. Это поле проявляет себя в том, что помещенный в какую-либо его точку электрический заряд оказывается под действием силы.

Представление об электрическом поле было введено в науку в 30-х годах XIX столетия английским учеными Майклом Фарадеем.

Согласно Фарадею, каждый электрический заряд окружен созданным им электрическим полем, поэтому такой заряд иногда называют зарядом- источником. Заряд, с помощью которого исследуют поле заряда источника, называют пробным зарядом.

Для того чтобы сила, действующая на пробный заряд, характеризовала поле в данной точке, пробный заряд должен быть точечным.

Точечным зарядом называют заряженное тело, размерами которого можно пренебречь в условиях данной задачи, т.е. размеры которого малы по сравнению с расстояниями до других тел, с которыми он взаимодействует. При этом собственное электрическое поле пробного заряда должно быть столь мало, чтобы оно не изменяло поле заряда - источника. Чем меньше размер заряженного тела и чем слабее его собственное поле по сравнению с полем заряда - источника, тем точнее данное заряженное тело удовлетворяет условию пробного заряда.

Электрическое поле распространяется в вакууме со скоростью с= 3·1⁸.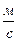

Поле неподвижных электрических зарядов - электростатическое.

Исследуем с помощью пробного заряда 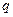поле, создаваемое неподвижным зарядом - источником 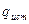(рис. 3).

Сила, действующая на пробный заряд в данной точке поля, зависит от величины пробного заряда. Если брать различные пробные заряды, то и сила, действующая на них в данной точке поля, будет различной.

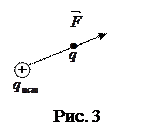Однако отношение силы к величине пробного заряда остается постоянным и характеризует уже само поле. Это отношение называется напряженностью электрического поля в данной точке.

, .

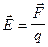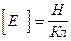Напряженность электрического поля - это векторная величина, численно равная силе, с которой поле действует на единичный положительный пробный заряд в данной точке поля и сонаправленная с этой силой.

Напряженность является основной характеристикой поля и полностью характеризует поле в каждой его точке по величине и направлению.

Напряженность поля точечного заряда.

Согласно закону Кулона

,

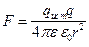поэтому

=.

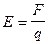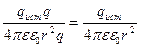Следовательно, напряженность электрического поля точечного заряда 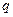на расстоянии r от этого заряда выражается формулой:

.

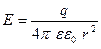Электрическое поле удобно графически изображать с помощью картины так называемых силовых линий или линий напряженности.

Линией напряженности называется линия, касательная к которой в каждой точке совпадает по направлению с вектором напряженности в этой точке.

Линии напряженности поля, создаваемого неподвижными зарядами (рис. 4, а, б), всегда начинаются и кончаются на зарядах (или в бесконечности) и никогда не бывают замкнутыми. Более сильное поле изображается более плотно расположенными линиями напряженности. Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности площадки, перпендикулярной к линиям, было равно численному значению вектора 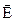. Линии напряженности никогда не пересекаются, т.к. их пересечение означало бы два различных направления вектора напряженности поля в одной и той же точке, что не имеет смысла.

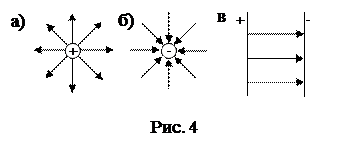Однородным называется поле, в котором напряженность во всех точках имеет одну и ту же величину и одинаковое направление, 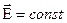. В таком поле силовые линии параллельны и плотность их всюду одинакова, т.е. они расположены на одинаковом расстоянии друг от друга (рис. 4, в).

Принцип суперпозиции.

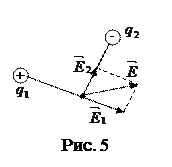Если электрическое поле в данной точке создано несколькими зарядами, то напряженность результирующего поля равна векторной сумме напряженностей полей, созданных каждым зарядом в отдельности (рис. 5).

,

.

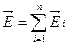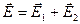Принцип суперпозиции является опытным фактом, справедливым вплоть до очень сильных полей. Поэтому же закону складываются не только статические, но и быстро меняющиеся электромагнитные поля.

Выделим в векторном поле 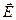некоторый объем, ограниченный поверхностью S. Разобьем эту поверхность на элементарные площадки величиной 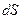(рис. 6).

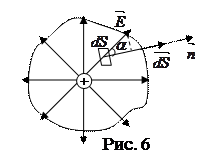Можно ввести в рассмотрение направленный элемент поверхности 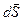. Направленным элементом поверхности 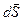называется вектор, длина которого равна площади элемента 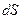, а направление совпадает с направлением нормали к этому элементу. Для замкнутой поверхности берется внешняя нормаль к поверхности. Поскольку выбор направления 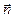произволен (условен), его можно направить как в одну сторону от площадки, так и в другую, 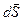является не истинным вектором, а псевдовектором.

Потоком 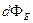вектора напряженности 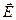через элементарную поверхность dS называется скалярное произведение

,

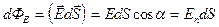где a- угол между векторам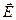и и ,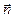

Е_п - проекция 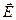на направление нормали .

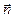Просуммировав потоки через все элементарные площадки, на которые разбили поверхность S, получим поток вектора 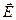через поверхность S.

Потоком вектора 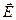через поверхность S называется интеграл

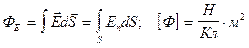
Для замкнутой поверхности .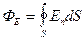

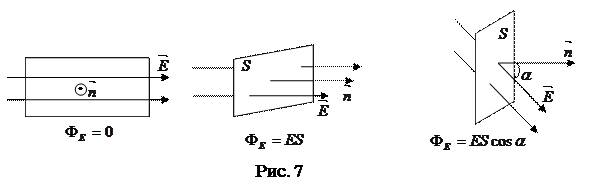Поток вектора - алгебраическая величина:

если

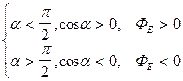
Для однородного поля 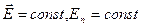(рис. 7),

.

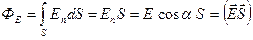Потоку вектора напряженности можно дать наглядную геометрическую интерпретацию: 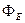численно равен количеству линий напряженности, пересекающих данную поверхность.

3. Теорема Гаусса для потока вектора 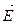и ее применение для расчета полей протяженных зарядов в вакууме.

Зная напряженность поля точечного заряда и используя принцип суперпозиции, можно рассчитать напряженность поля, созданного несколькими точечными зарядами. Однако для протяженных зарядов применение принципа суперпозиции затруднительно. Метод расчета полей, созданных протяженными зарядами, был предложен немецким ученым Гауссом в начале 19 века.

Теорема Гаусса для электростатического поля в вакууме.

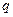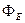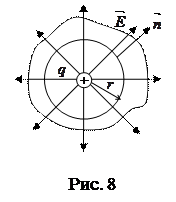
Рассмотрим поле точечного заряда в вакууме и вычислим через поверхность сферы радиуса 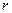(рис. 8).

.

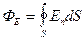Напряженность поля в любой точке поверхности сферы

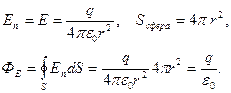
Т.к. 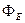численно равен числу линий вектора 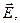пересекающих эту поверхность, то, если вместо сферы взять любую другую замкнутую поверхность, поток останется тем же, т.к. все линии, проходящие через сферу, проходят и через эту поверхность. Таким образом, для любой замкнутой поверхности, заключающей в себе точечный заряд q

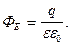
Если внутри замкнутой поверхности находятся N точечных зарядов, то согласно принципу суперпозиции:

если 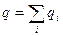, то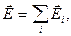

поэтому ,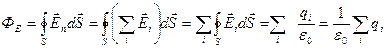

т.к. каждый интеграл .

Теорема Гаусса для электростатического поля в вакууме: .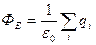

Поток вектора напряженности электростатического поля в вакууме через любую замкнутую поверхность прямо пропорционален алгебраической сумме зарядов, охватываемых этой поверхностью.

Суть метода Гаусса:

1) охватывать участок, содержащий заряды, замкнутой поверхностью;

2) выразить Ф_Е через эту поверхность;

3) выразить суммарный заряд через t или s;

4) приравнять Ф_Е суммарному заряду, деленному на e₀;

5) из полученного соотношения найти Е.

Поле бесконечной равномерно заряженной плоскости.

Поверхностная плотность заряда - физическая величина, равная заряду, приходящемуся на единицу площади равномерно заряженной поверхности.

.

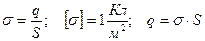Если поверхность заряжена неравномерно,

.

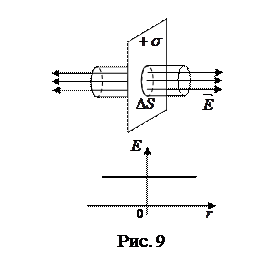
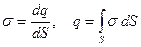Поле такой поверхности однородно. Окружим элемент DS этой поверхности замкнутой поверхностью в форме цилиндра (рис. 9). 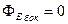- поток 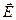через боковую поверхность равен нулю, т.к. линии 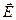не пересекают ее.

,

; .

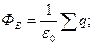
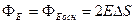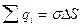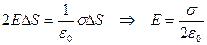Поле 2-х бесконечных разноименно заряженных плоскостей (рис. 10).

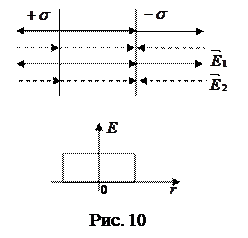
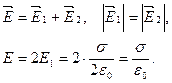
Полученный результат справедлив для плоскостей конечных размеров, расстояние между которыми мало по сравнению с их размерами (конденсатор).

Поле бесконечного равномерно заряженного цилиндра (рис. 11).

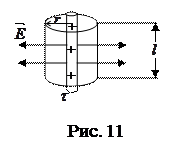Линейная плотность заряда - физическая величина, численно равная заряду, приходящемуся на единицу длины равномерно заряженной нити.

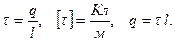
Если нить заряжена неравномерно,

;

.

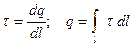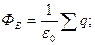
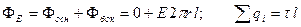
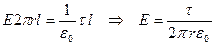Поле равномерно заряженной сферы радиуса R (рис. 12).

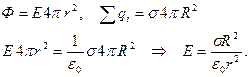
Дата добавления: 2014-01-07