Прямая в пространстве

12.1 Канонические уравнения прямой в пространстве. Договоримся называть любой ненулевой вектор, параллельный данной прямой, направляющим вектором этой прямой. Выведем уравнение прямой, проходящей через данную точку 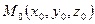и параллельную данному направляющему вектору 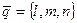. Заметим, что точка 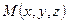лежит на этой прямой тогда и только тогда, когда векторы 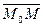и 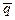коллинеарны. Это означает, что координаты этих векторов пропорциональны:

.

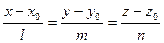Эти уравнения называют каноническими. Заметим, что одна или две координаты направляющего вектора могут оказаться равными нулю. Но мы воспринимаем это как пропорцию: 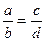мы понимаем как равенство .

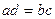12.2. Параметрические уравнения прямой в пространстве. Откладывая от точки 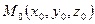векторы 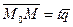для различных значений 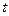, коллинеарные направляющему вектору, мы будем получать на конце отложенных векторов различные точки нашей прямой. Из равенства 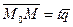следует:

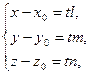
или

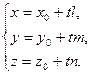
Переменную величину 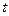называют параметром. Поскольку для любой точки прямой найдется соответствующее значение параметра и поскольку различным значениям параметра соответствуют различные точки прямой, то существует взаимно однозначное соответствие между значениями параметра и точками прямой. Когда параметр 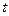пробегает все действительные числа от 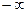до 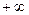, соответствующая точка 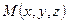пробегает всю прямую.

Очевидна механическая интерпретация параметрических уравнений. Если считать, что 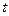- это время, 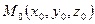- начальное положение точки при 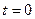, вектор 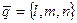- постоянный вектор скорости, то параметрические уравнения описывают закон равномерного движения точки.

Параметрические уравнение легко получаются из канонических уравнений: достаточно лишь приравнять три отношения, участвующие в канонических уравнениях, к параметру .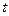

12.3. Уравнения прямой, проходящей через две данные точки. Пусть даны две точк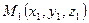и и 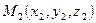. Чтобы найти канонические уравнения прямой, проходящей через эти точки, заметим, что вектор 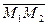является направляющим вектором этой прямой. Тогда искомые уравнения имеют вид:

.

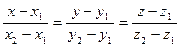12.4. Угол между двумя прямыми. Задача нахождения угла между двумя прямыми сводится к нахождению угла между их направляющими векторами. Если прямые заданы своими каноническими уравнениям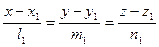и

и ,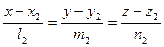

то векторы 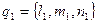и 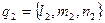являются их направляющими векторами. Тогда косинус угла между прямыми можно найти, используя скалярное произведение:

.

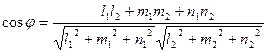Прямые параллельны, если коллинеарны их направляющие векторы:

.

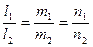Прямые перпендикулярны, если перпендикулярны их направляющие векторы, т.е. их скалярное произведение равно нулю:

.

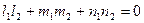12.5. Взаимное расположение двух прямых в пространстве. В пространстве взаимное расположение двух прямых может быть следующим: 1) эти прямые параллельны (в частности, совпадают), 2) они пересекаются, 3) они скрещиваются. В первых двух случаях прямые лежат в одной плоскости. Найдем, когда две прямые принадлежат одной плоскости. Пусть эти прямые заданы своими каноническими уравнениям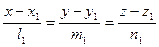и и 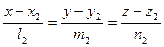, Рассмотрим три вектора: 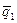, 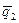и 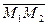. Для того, чтобы прямые принадлежали одной плоскости, необходимо и достаточно, чтобы эти векторы были компланарны. Это выполняется тогда и только тогда, когда смешанное произведение этих трех векторов равно нулю, т.е 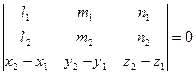. Если при этом координаты направляющих векторов пропорциональны, то эти прямые параллельны.

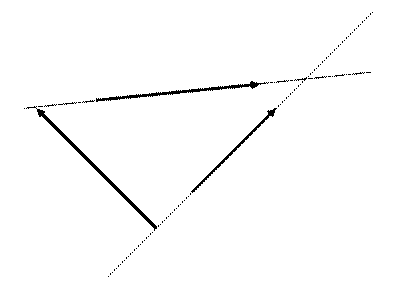
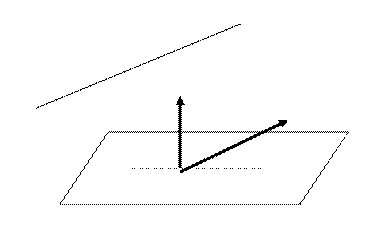
12.6. Взаимное расположение прямой и плоскости. Пусть нам заданы прямая

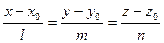
и плоскость 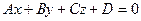. Так как угол 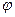между прямой и плоскостью и угол 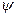между прямой и нормальным вектором к плоскости связаны очевидным равенством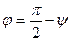, то 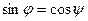. Поэтому

.

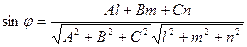Условие перпендикулярности прямой и плоскости соответствует коллинеарности направляющего вектора прямой и нормали к плоскости.

Условие параллельности прямой и плоскости – или перпендикулярности прямой и нормального вектора к плоскости - можно записать в виде 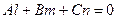. Частный случай параллельности – прямая принадлежит плоскости – выполняется, если еще и какая-нибудь точка прямой принадлежит плоскости, например, выполняется равенство .

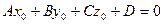12.7. Расстояние от точки до плоскости. Пусть нам заданы точка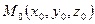

и плоскость 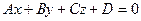. Проведем через точку 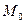прямую, перпендикулярную плоскости. Заметим, что вектор нормали к плоскости может служить направляющим вектором этой прямой:

.

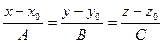Перейдем к параметрическим уравнениям:

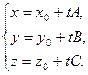
Найдем, при каком значении параметра точка прямой будет принадлежать плоскости. Для этого подставим параметрические уравнения прямой в уравнение плоскости и решим получившееся уравнение относительно :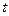

Расстояние от точки 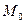до точки, соответствующей этому значению параметра, равно длине вектора 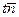. Нам осталось найти эту длину:

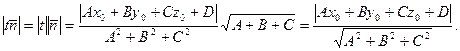
Это и есть расстояние от точки 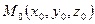до плоскости.

Дата добавления: 2014-01-07