
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Неравенство Чебышева. Моменты случайной величины Определение 12.3 Для целого неотрицательного начальным моментом порядка k называется величина
Моменты случайной величины
| Определение 12.3 | Для целого неотрицательного  начальным моментом порядка k называется величина начальным моментом порядка k называется величина
 . .
|
| Определение 12.4 | Для целого неотрицательного  центральным моментом порядка k называется величина центральным моментом порядка k называется величина
 . .
|
| Теорема 12.1. Неравенство Чебышева | Пусть 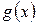 — неотрицательная неубывающая на множестве значений случайной величины — неотрицательная неубывающая на множестве значений случайной величины 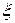 функция. Предположим, что существует функция. Предположим, что существует  . Тогда для каждого . Тогда для каждого 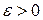 справедливо справедливо
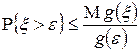 . .
|
Доказательство. Пусть  — функция распределения
— функция распределения 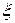 . Применяя формулу (12.1), получим
. Применяя формулу (12.1), получим
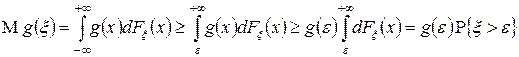 ,
,
 что и доказывает теорему.
что и доказывает теорему.
ЧЕБЫШЕВ ПАФНУТИЙ ЛЬВОВИЧ (14 (26) мая 1821, село Окатово Калужской губернии, ныне Калужской области — 26 ноября (8 декабря) 1894, Санкт–Петербург) — российский математик и механик, член Петербургской академии наук (1856), основатель Петербургской математической школы. Член Берлинской АН (1871), Болонской АН (1873), Парижской АН (1874; член-корреспондент с 1860), Лондонского Королевского общества (1877), Шведской АН (1893) и почетный член многих русских и иностранных научных обществ, академий, университетов.
П.Л. Чебышёв положил начало развитию многих новых разделов математики (теория приближений функций, интегральное исчисление, теория чисел, теория вероятностей), а также теории механизмов и машин. Одним из первых он начал увязывать проблемы математики с принципиальными вопросами естествознания и техники, многие его открытия обусловлены именно прикладными задачами.
В 1847 защищает в Петербургском университете диссертацию «Об интегрировании с помощью логарифмов» на право чтения лекций и после утверждения в звании доцента приступает к чтению лекций по алгебре и теории чисел. В 1849 защищает в Петербургском университете докторскую диссертацию «Теория сравнений», которая в том же году была удостоена Демидовской премии. С 1850 по 1882 — профессор Петербургского университета. После выхода в отставку Чебышев до конца жизни занимается научной работой.
С 1856 года Чебышев работал в артиллерийском отделе Военного ученого комитета, занимался вопросами баллистики. Его теоретические разработки позволили русской артиллерии выйти в конце 19 века на одно из первых мест в мире.
Исследования Чебышева относятся к теории приближения функций многочленами, интегральному исчислению, теории чисел, теории вероятностей, теории механизмов и другим областям знания. Наибольшее число работ посвящено математическому анализу.
Работы Чебышева по теории вероятностей: «Опыт элементарного анализа теории вероятностей» (1845); «Элементарное доказательство одного общего положения теории вероятностей» (1846); «О средних величинах» (1867); «О двух теоремах относительно вероятностей» (1887)] ознаменовали важный этап в развитии теории вероятностей. П.Л.Чебышев стал систематически использовать случайные величины. Им доказаны неравенство, носящее ныне имя Чебышева, и — в весьма общей форме — закон больших чисел.
В 1944 Академией наук СССР учреждена премия имени П.Л.Чебышева.
12.5. Неравенство Иенсена [1]
| Теорема 12.2. Неравенство Иенсена | Пусть 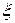 — случайная величина с областью значений — случайная величина с областью значений  , а , а 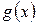 — выпуклая вниз на — выпуклая вниз на 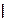 функция. Тогда справедливо функция. Тогда справедливо
 . .
|
Доказательство. Из курса математического анализа известно, что функция 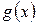 выпуклая на
выпуклая на 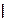 тогда и только тогда, когда
тогда и только тогда, когда

в каждой точке 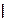 . Запишем разложение в ряд Тейлора функции
. Запишем разложение в ряд Тейлора функции 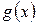 в окрестности точки
в окрестности точки 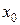 с остаточным членом в форме Лагранжа
с остаточным членом в форме Лагранжа
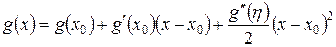 ,
,
где 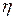 точка, лежащая между
точка, лежащая между  и
и 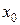 . Так как
. Так как 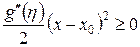 , то
, то
 .
.
Положим 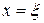 и
и 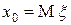 :
:
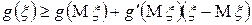 .
.
Возьмем математическое ожидание от обеих частей последнего неравенства, в результате получим
 .
.
Что и требовалось доказать.
|
Дата добавления: 2014-01-07; Просмотров: 632; Нарушение авторских прав?; Мы поможем в написании вашей работы!