Задачи и упражнения. 1. Вычислить дисперсию геометрически распределенной случайной величины

1. Вычислить дисперсию геометрически распределенной случайной величины.

2. Вычислить дисперсию случайной величины, распределенной по закону Пуассона.

3. Случайная величина 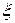имеет гипергеометрическое распределение с параметрами , если

, .

Найти математическое ожидание и дисперсию случайной величины .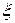

4. Случайная величина 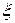имеет распределение Бореля–Таннера с параметрами , если

,

5. Вычислить математическое ожидание и дисперсию случайной величины, у которой

, .

6. Доказать, что дисперсия числа появлений события при однократном производстве опыта не превосходит .

7. Вычислить дисперсию случайной величины, подчиняющейся закону Лапласа, с плотностью

.

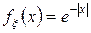8. Вычислить дисперсию нормальной с параметрами случайной величины.

9. Определить условия, при которых третий центральный момент биномиального распределения равен нулю.

10. Случайная величина 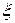подчиняется бета распределению, то есть имеет плотность распределения вероятностей

, .

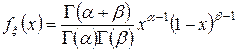Найти начальный момент –го порядка.

11. Выразить центральный момент через начальные моменты.

12. Выразить начальный момент через центральные моменты и математическое ожидание.

13. Случайная величина 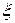равномерно распределена на отрезке . Найти:

а) , , , ;

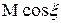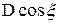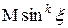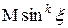б) , при любом целом и асимптотику , при .

14. Случайная величина 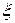равномерно распределена на отрезке . Найти:

а) , , , ;

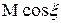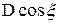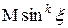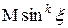б) , при любом целом и асимптотику , при .

15. Вероятность появления события 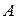при одном опыте равна 0,4; оценить с помощью неравенства Чебышева вероятность того, что частота этого события при 100 опытах будет лежать в пределах 0,3–0,5.

16. Среднее квадратическое отклонение ошибки измерения курса самолета равно 20. Считая математическое ожидание ошибки измерения равным 0, оценить вероятность того, что ошибка при данном измерении курса будет более 50.

[1] Иенсен Иоганн Людвиг [Jensen Johann Ludwig] (1859–1925) — датский математик. Основные труды по теории функций. Неравенство Иенсена (1906).

[2] Гельдер Людвиг Отто [Hölder Ludwig Otto] (1859–1937) —немецкий математик. Основные труды в области алгебры, математического анализа, оснований математики.

Дата добавления: 2014-01-07