Алгебраические структуры с двумя бинарными операциями

ЛЕКЦИЯ 12

Историко-культурологическое изучение антропогенного ландшафта

Геоэкологическим анализом изучение антропогенных ландшафтов не исчерпывается. Наряду с ним применяется этно-исторический и культурологический подходы. В последние годы историко-культурологическая концепция антропогенного ландшафта получила новый импульс развития в связи с происходящей в наше время гуманизацией ландшафтоведения [23]. Согласно этой концепции, освоенные человеком ландшафты во многом представляют собой продукт истории населяющих их народов, их материальной и духовной культуры. При этом антропогенный ландшафт рассматривается как своего рода отражение, отпечаток преобразующего его социума. Установлена закономерность: каково общество, его культура, менталитет и исторические судьбы, таков и ландшафт, им созданный. Ландшафт - лицо страны, лицо нации. Как по состоянию и убранству квартиры или дома можно судить о хозяевах, так по антропогенному ландшафту - о культуре, трудовых навыках и традициях его социума. Если архитектура старинных городов расценивается как история, запечатленная в камне, то антропогенный ландшафт в не меньшей мере читается как историческая летопись.

При классификации антропогенных ландшафтов должны учитываться не только их природная и производственная подсистемы, но вместе с тем и социально-культурная. Есть основания говорить о национальных ландшафтах: испанских и французских, немецких и польских, финских и карельских, израильских и палестинских. Несмотря на географическое соседство и сходство природных условий, имсвойственна ярко выраженная этнокультурная специфика.

При пересечении границы России и стран Балтии бросаются в глаза поразительные различия в облике сельских ландшафтов и провинциальных городов названных стран. И это, несмотря на полное сходство природных условий. Ухоженный западноевропейский ландшафт Балтии невозможно спутать с северо-западным российским, лишенным европейского лоска.

В полупустыне северного Прикаспия рубеж России и Казахстана отмечен не пограничными столбами, а резкой сменой сельского ландшафта. В волгоградском Заволжье его распаханность достигает 50-70%, тогда как в Западном Казахстане - не превышает 20%. Русские переселенцы в начале XX века привнесли в эти аридные края культуру земледелия; местные казахи - продолжают придерживаться традиционного пастбищного животноводства.

Кольцо, определение, простейшие свойства

Знакомство с алгебраическими структурами, порождаемыми множеством с заданной на нем одной бинарной операцией, привело нас к понятиям группоида, моноида, группы, причем в качестве знака бинарной операции у нас фигурировали операции сложения "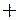" и умножения "×".

Естественно, рассмотреть множества с заданными на них двумя бинарными операциями "×", "".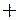

Рассмотрение таких множеств приводит к расширению свойств рассматриваемых множеств, а также к ряду новых понятий, основными из которых теперь уже будут

кольца, тела, идеалы, поля.

Начнем с простейшего.

Определение. Пусть X – непустое множество-носитель, на котором заданы две бинарные алгебраические операции: сложение "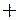" и умножение "×", тогда 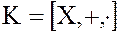– называется кольцом, если удовлетворяются три следующих условия:

1. 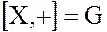– аддитивная абелева группа, для которой выполняются аксиомы группы:

· замкнутость: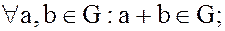

· ассоциативность: ;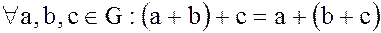

· наличие единичного элемента:

;

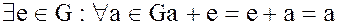· наличие обратного элемента:

;

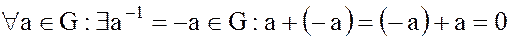· коммутативность: .

2. – мультипликативная полугруппа, для которой выполняются:

· замкнутость: ;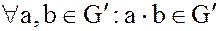

· ассоциативность: .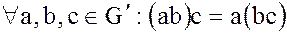

3. Операции сложения "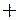" и умножения "×" связаны дистрибутивными законами по "":

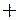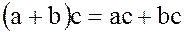· – дистрибутивность слева;

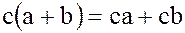· – дистрибутивность справа.

Замечания. 1. Единичный элемент группы 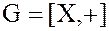кольца 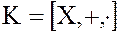называется нулевым элементом кольца и обозначается 0.

2. Из определения кольца не следует существование или отсутствие в кольце единичного (относительно операции умножения) элемента. Однако, если в кольце существует единичный элемент, то он единственный. Если 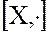– моноид, т.е. полугруппа с единицей, то кольцо 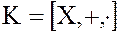– называется кольцом с единицей.

3. Единичный элемент кольца обозначается 1.

Определение. Если , то кольцо называется коммутативным (его не принято называть абелевым).

Определение. Кольцо, элементами которого являются числа, называется числовым кольцом.

Определение. Кольцо 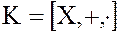называется конечным, если множество его элементов 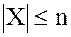конечно.

Примеры числовых колец.

1. Коммутативное кольцо целых чисел .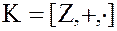

2. Коммутативное кольцо рациональных чисел .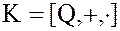

3. Коммутативное кольцо четных целых чисел .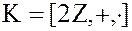

4. Коммутативное кольцо действительных чисел .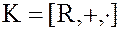

5. Обозначим 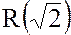множество всех чисел вида , где 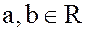– любые рациональные числа.

Покажем, что 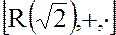является коммутативным кольцом относительно операций сложения и умножения действительных чисел.

Действительно, для любых двух чисел 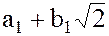и 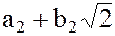из множества 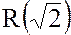, их сумма

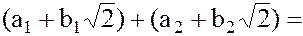
и произведение

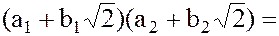
– принадлежат множеству ;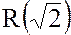

число 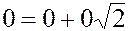содержится в ;

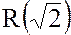для любого числа из 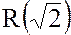обратное (противоположное) ему число

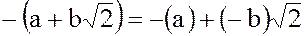
принадлежит множеству .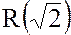

Так как операции сложения и умножения действительных чисел ассоциативны и коммутативны, то операции сложения и умножения элементов множества 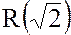также ассоциативны и коммутативны, а операция умножения на множестве 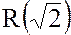дистрибутивна относительно операции сложения.

Следовательно, 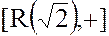– абелева группа, 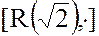– полугруппа, 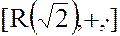– коммутативное кольцо.

Замечание. 1. К кольцу 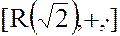принадлежат, в частности, все рациональные числа (при 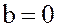), а также число 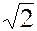(при , ).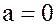

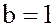2. Вместо числа 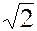можно было бы взять и другие числа, например, 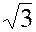,,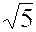, 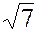но тогда мы имели бы другие кольца.

3. Нулевое кольцо 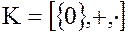состоит из одного элемента – числа нуль. Во всех рассмотренных примерах элементами кольца являются числа.

Примеры не числовых полей.

1. Пусть – множество всех квадратных матриц порядка 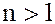с вещественными коэффициентами. Тогда – кольцо квадратных матриц с нулем 0 и единицей Е.

Действительно, – абелева группа, 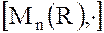– некоммутативная полугруппа.

Определение. Множество – называется полным матричным кольцом над R или кольцом квадратных матриц порядка 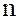над R.

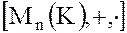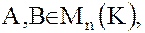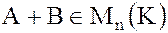Замечание. Пусть К – некоторое коммутативное кольцо. Тогда – также кольцо матриц с элементами из К. Действительно, если то и 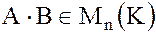, т.е. при сложении и умножении матриц с элементами из К мы вновь будем получать матрицы с элементами из К.

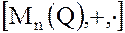– кольцо матриц с рациональными коэффициентами (или над Q).

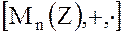– кольцо матриц с целыми коэффициентами (или над Z).

2. Кольцо функций, заданных на произвольном множестве X со значениями в произвольном кольце K.

Пусть X – произвольное множество, К – произвольное кольцо. Тогда 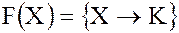– множество всех функций, или множество всех однозначных отображений , рассматриваемых вместе с двумя бинарными операциями – поточечной суммой 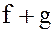и поточечным произведением 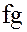, определяемых следующим образом:

;

,

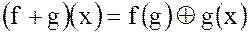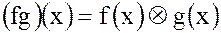где – операции сложения и умножения в кольце К.

Замечание. Особую роль в математическом анализе играет случай, когда . В этом случае говорят о кольце функций одной переменной.

Произведением функций 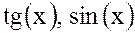, будет

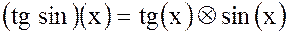, но не .

Можно показать, что в 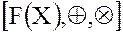выполняются все аксиомы кольца.

Нулевым и единичным элементами в кольце 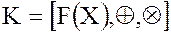являются постоянные функци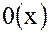и и :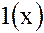

– нулевая функция, принимающая тождественно значение "0";

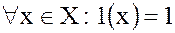– единичная функция, принимающая тождественно значение "1".

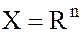Если или 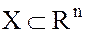, то говорят о кольце функций n–переменных.

Дата добавления: 2014-01-07