Элементарные свойства колец

Многие свойства колец являются переформулировками соответствующих свойств групп или более точно – множеств с одной бинарной операцией.

Из ассоциативности операции умножения вытекают следующие свойства кольца:

· в каждом кольце К произведение любых n его элементов не зависит от способа расстановки скобок;

· в каждом кольце К содержатся целые положительные степени любого его элемента , причем для 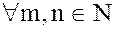справедливы следующие равенства:

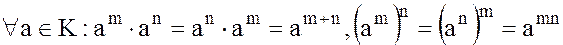. (1)

Единственным условием в определении кольца, связывающим операции сложения и умножения, является дистрибутивность умножения относительно сложения.

Из дистрибутивности операции умножения относительно операции сложения непосредственно вытекает справедливость следующих теорем.

Теорема 1. В любом кольце К дистрибутивные законы справедливы для любого конечного числа слагаемых:

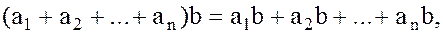(2)

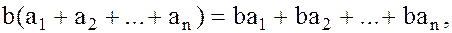(3)

для любого .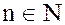

Доказательство. Доказательство справедливости равенств (2) и (3) аналогичны. Поэтому докажем справедливость только равенства (2).

При 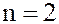равенство (2) справедливо. Предположим, что равенство (2) справедливо и при 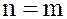и докажем, что оно справедливо и при .

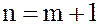Пусть

.

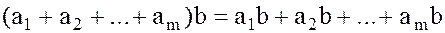Тогда

.

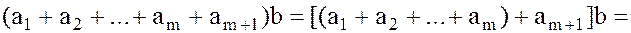
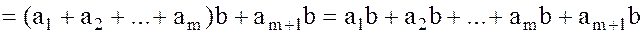Следовательно, в силу принципа математической индукции, равенство (2) справедливо для .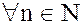

Теорема 2. (Обобщенная дистрибутивность) В любом кольце К справедливо обычное правило умножения суммы на сумму (но без изменения порядка множителей):

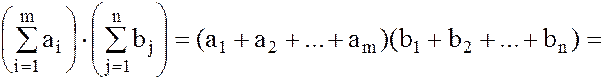
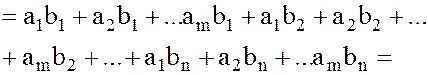
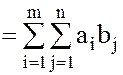. (4)

Доказательство. По предыдущей теореме имеем:

.

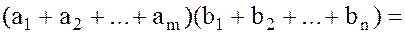
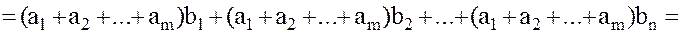
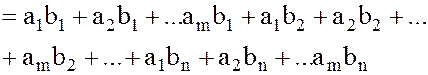Теорема 3. (Операция вычитания) В любом кольце К для 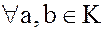существует единственное решение уравнения

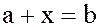
Это решение называется разностью элементов b и a и обозначается b – a, а операция «–» называется операцией вычитания. Поскольку решением уравнения 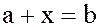является элемент 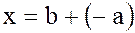, то, следовательно,

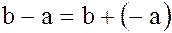. (5)

Теорема 4. В любом кольце К операция умножения дистрибутивна относительно операции вычитания:

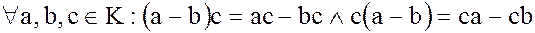. (6)

Доказательство. Действительно, 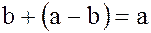. Поэтому 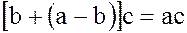. Отсюда, по закону дистрибутивности операции умножения относительно операции сложения, имеем 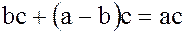. По определению разности 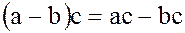. Аналогично доказывается и справедливость равенства .

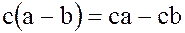Теорема 5. (Умножение на нуль) В любом кольце 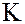произведение любого его элемента на нуль и нуля на элемент равно нулю:

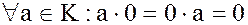(7)

Доказательство. Так как любое кольцо 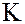по операции сложения - абелева группа, то 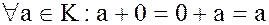. Умножая полученное равенство справа и слева на 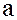, имеем:

.

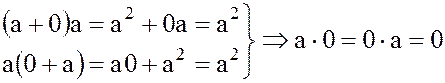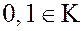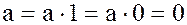Пусть предположим на момент, что , тогда мы получаем для .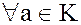

Это означает, что кольцо 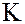в этом случае является тривиальным и состоит только из одного элемента – нуля. Следовательно, в нетривиальном кольце 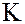всегда .

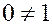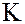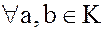Теорема 6. (Правило знаков). В любом кольце для справедливы следующие равенства:

(8)

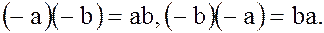(9)

Доказательство. Докажем (8). Действительно,

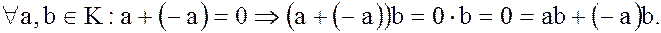
Таким образом, элемент 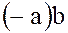является обратным (противоположным) к элементу 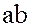и следовательно, .

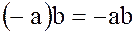С другой стороны,

.

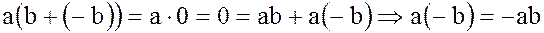Докажем (9). Учитывая, что 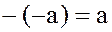, а также равенство (8) получаем

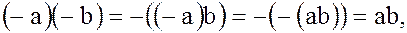
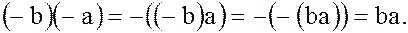
Замечание. Несмотря на всю очевидность этих свойств для числовых колец, не следует думать, что всякое свойство операций сложения и умножения чисел сохраняется для бинарных операций в произвольном кольце. Те свойства операций сложения и умножения чисел, которые не являются следствиями из аксиом кольца, в произвольном кольце могут и не иметь места. Более подробно мы остановимся на этом далее.

Дата добавления: 2014-01-07