Температурная зависимость упругости насыщенных паров

Было сказано, что с повышением температуры упругость насыщенного пара растет. Найти эту температурную зависимость можно, воспользовавшись законом Больцмана.

Молекулы, покидающие жидкость при испарении, совершают работу против сил притяжения со стороны других молекул жидкости. При переходе в пар их энергия изменяется на величину совершенной работы. Средняя энергия молекулы, вылетевшей из жидкости, отличается от энергии молекулы, находящейся внутри жидкости, на величину , где L – молярная скрытая теплота испарения. Если не учитывать работу, которую совершают эти молекулы против сил давления пара, то величина и есть та энергия, которая входит в показатель экспоненты в законе Больцмана. Поэтому плотность молекул пара определяется равенством:

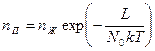
где 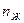- плотность молекул жидкости, потенциальную энергию которых принимаем равной нулю. Из МКТ известно, что плотность молекул пара равна 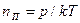. Подставляя это выражение и разрешая его относительно давления,

получим:

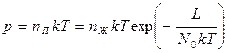
Это уравнение и определяет температурную зависимость упругости насыщенного пара. При более строгом рассмотрении необходимо учитывать, что входящие в него величины L и n_ж сами зависят от температуры. Для практического использования удобно пользоваться другой формой записи. После логарифмирования получим: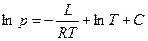, где - константа, характерная для данной жидкости. Так как 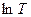есть медленно изменяющаяся функция температуры, то в первом приближении можно считать, что 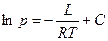. При графическом изображении этой функции удобно пользоваться координатам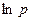и и 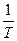(рис45). 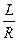Тогда получается прямая линия, где тангенс угла наклона равен отношению , поэтому, пользуясь экспериментальным графиком можно определить значение молярной скрытой теплоты испарения исследуемой жидкости.

Полученная зависимость носит приближенный характер по двум причинам: а) не учитывалась работа, совершаемая молекулой против давления уже существующего пара и б) игнорировалась величина 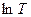. Но аналогичные рассуждения можно провести с термодинамических позиций.

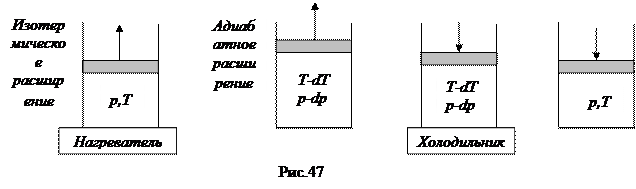Проведем мысленно круговой процесс Карно, в котором рабочим веществом является исследуемая жидкость. Пусть исходное состояние характеризуется температурой Т и давлением р, и пусть при этом жидкость заполняет весь объем сосуда (паровой фазы нет). Это состояние отражается точкой А на горизонтальной части изотермы реального газа (рис.46,47). Соответствующий температуре Т молярный объем V₁. Практически это означает, что жидкость находится в цилиндре с поршнем, который приведен в контакт с нагревателем. За счет теплоты нагревателя жидкость начинает испаряться, в результате чего поршень поднимается – происходит изотермическое расширение пара. Давление при этом сохраняется прежним, так как пар насыщенный. Пусть процесс продолжается до тех пор, пока не испариться один моль жидкости. Для этого от нагревателя будет заимствовано количество теплоты, равное молярной скрытой теплоте испарения: . В результате объем увеличится до значения V₂, занимаемого одним молем пара при давлении р и температуре Т. Это состояние отвечает точке В. После этого система изолируется и производится дополнительное адиабатное расширение так, чтобы температура газа понизилась на dT и давление на dp. Это участок цикла ВС. Точка С соответствует состоянию пара при давлении p-dp и температуре T-dT. В этом состоянии система приводится в контакт с холодильником, обладающим температурой T-dT. Производится изотермическое сжатие пара при постоянном давлении p-dp до полной конденсации (точка D). При этом часть теплоты Q₁ перейдет холодильнику. Затем система вновь изолируется и дополнительным адиабатным сжатием давление и температура приводятся к исходным значениям.

Работа, произведенная за цикл равна площади ABCD, которую приближенно можно считать равной площади параллелограмма: . Отношение полученной работы к затраченной теплоте есть кпд цикла.

. С другой стороны, тот же кпд равен: 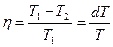. Приравнивая их, получим: 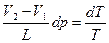, или 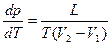. Это уравнение, выражающее зависимость упругости насыщенного пара от температуры называется уравнением Клапейрона – Клаузиуса. Оно справедливо не только для перехода жидкость – пар, но и для всех других фазовых переходов, выражая зависимость изменения давления, при котором фазы находятся в равновесии, от изменения температуры.

Испарение происходит с поверхности жидкости, поэтому любое изменение свойств поверхности должно сказываться на условиях равновесия между паром и жидкостью. В частности, на условиях равновесия, а, значит, на упругости насыщенного пара должна сказываться кривизна поверхности жидкости. Это следует из общих соображений. При испарении с плоской поверхности ее поверхностная энергия не меняется, поскольку остается неизменной ее площадь. Другое дело, когда испаряется, например, сферическая капля. По мере испарения уменьшается объем капли, а, следовательно, ее поверхность. Уменьшается поверхностная энергия жидкости в капле. А так как всякая система стремиться перейти в состояние равновесия, при котором энергия ее минимальна, совершив, при этом, соответствующую работу, то каплю следует считать неустойчивой системой. При определенных условиях, например, если в замкнутом сосуде находится жидкость с плоской поверхностью и сферическая капля жидкости, то равновесие установится только после того, как капля полностью испарится и сконденсируется на плоской поверхности. Это означает, что упругость насыщенного пара над сферической каплей больше, чем над плоской поверхностью остальной жидкости.

Это относится не только к сферическим каплям, но и ко всякой жидкости с выпуклой поверхностью. Над вогнутой поверхностью упругость насыщенных паров, наоборот, меньше, чем над плоской поверхностью. Разность упругостей паров над плоской и кривой поверхностями можно вычислить следующим образом.

Пусть в закрытом сосуде находится жидкость, в которую погружена капиллярная трубка, полностью смачиваемая жидкостью (рис.48). Жидкость поднимется на высоту: . Так как сосуд закрытый, то над вогнутой и плоской поверхностями жидкости в состоянии равновесия должен находиться насыщенный пар. Но давление насыщенного пара над вогнутой поверхностью должно быть меньше, чем над плоской. Т.е. давление насыщенного пара на высоте h (у точки В) согласно барометрической формуле должно быть: 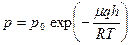. Если бы давление насыщенного пара над мениском в капилляре было таким же, как и над плоской поверхностью, то оно было бы больше, чем давление в окружающем пространстве, и возник бы непрерывный поток пара из капилляра, что сделало бы это устройство вечным двигателем. Следовательно давление насыщенного пара над мениском должно быть равно давлению пара в окружающем пространстве, т.е p, а не p₀. Подставив в последнее уравнение значение h из предыдущего, получим:

или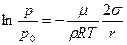

Это соотношение (между p и p₀) выражает отношение упругостей насыщенного пара над вогнутой и плоской поверхностями жидкости при одинаковой температуре.

Очевидно, что, поместив капилляр в несмачивающую жидкость, можно показать, что над выпуклой поверхностью давление ее насыщенного пара будет больше, чем над плоской, на ту же величину.

Различие в значениях давлений насыщенного пара над плоской и кривой поверхностями связано исключительно с кривизной поверхности. Ни сила тяжести, ни разность высот не играют роли. Поэтому полученная формула относится не только к случаю, когда поверхность кривая из-за того, что жидкость находится в капилляре, но и к таким случаям, как капли (выпуклая поверхность) и газовые пузырьки в жидкости (вогнутая поверхность жидкости).

То обстоятельство, что упругость насыщенных паров над выпуклой поверхностью выше, чем над плоской, играет существенную роль в различных явлениях, например, при образовании дождевых капель. В атмосфере часто создаются такие условия, когда парциальное давление паров воды превосходит упругость насыщенного пара при той же температуре. Для установления равновесия необходимо, чтобы пары сконденсировались. Однако начало процесса конденсации бывает затруднено, если воздух очень чистый. В самом начале конденсации образующиеся капли малы, следовательно, их поверхность имеет большую кривизну. Над такой сильно искривленной поверхностью упругость насыщенного пара должна быть намного выше нормальной. Например, при радиусе капли 10^-7м, отношение р/р₀=3, т.е. упругость насыщенного пара над поверхностью такой капли в 3 раза выше нормальной. Если она превышает парциальное давление пара, то капли будут испаряться быстрее, чем расти. Рост капель возможен только в том случае, если парциальное давление паров воды будет больше не только упругости насыщенного пара при той же температуре, но и упругости паров над поверхностью капли малого диаметра. Этим объясняется тот факт, что аэрозоли воздуха, на которых может начинаться конденсация, существенно облегчают ее, так как обеспечивают образующимся каплям начальный, достаточный для роста размер.

Дата добавления: 2014-01-07