Вязкостный режим

Течение газов через отверстия

Под отверстием понимается трубопровод, длина которого значительно меньше диаметра (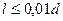), расположенный в стенке, разделяющей два бесконечно больших объема. Это отверстие называют диафрагмой, которая характеризуется толщиной (h). Различают большую диафрагму и малую. Рассмотрим поток газа через малую диафрагму (рис.15.2).

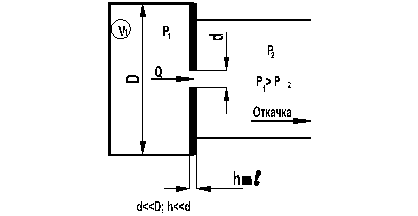
Рис.15.2. Малая диафрагма

По мере уменьшения давления Р₂ количество протекающего через диафрагму газа увеличивается (считаем, что Р₁ не изменяется), увеличивается и скорость потока в объем, где давление Р₂, до тех пор, пока отношение давлений 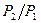не достигнет критического значения. При этом значении скорость потока через диафрагму достигает местной скорости звука и при дальнейшем уменьшении Р₂ увеличение скорости, а, следовательно и расхода, не происходит, т.е. устанавливается стационарное критическое течение через отверстие.

Для стационарного адиабатического течения невесомого газа запишем уравнение сохранения энергии в следующем виде

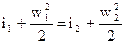
или

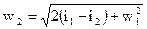, (12)

где w₁, w₂ – соответственно скорости потока в объеме V₁, и на выходе из диафрагмы, i₁, i₂ – соответствующие энтальпии.

Применительно к рассматриваемому случаю истечения w₁=0 и выражение (12) примет вид

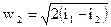. (13)

Рассмотрим процесс истечения на диаграммах i-s и PV (рис.15.3 и рис.15.4).

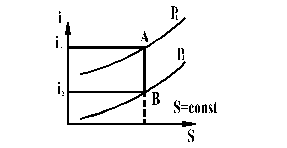
Рис.15.3. Процесс истечения газа через диафрагму

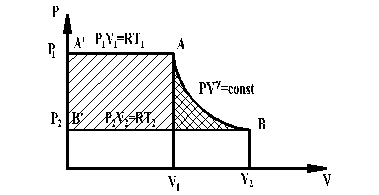
Рис.15.4. Процесс расширения газа и располагаемая работа

Преобразуем выражение (13)

, или 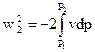, (14)

где - 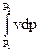- располагаемая работа (знак (-) потому, что P₁<P₂, т.е. верхний предел интегрирования меньше нижнего).

Так как процесс адиабатический, т.е. P и v связаны уравнением адиабаты 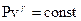, то

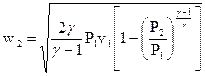, (15)

или с учетом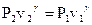

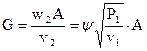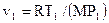, но и 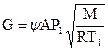, (16)

где А – площадь диафрагмы; ; ,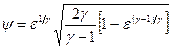

М – молекулярная масса, R – универсальная газовая постоянная.

Выразим поток газа в условных единицах (PV):

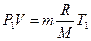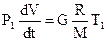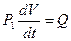; ; , Па×м³/с

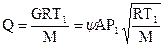. (17)

Проводимость диафрагмы (отверстия) в вязкостном режиме 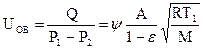. (18)

Критическое истечение определяется как 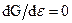, что приводит к нахождению e_k (критическое отношение давлений)

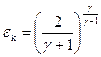. (19)

Для воздуха и других двухатомных газов g = 1,4. Тогда по (18)

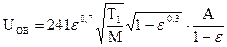. (20)

В выражении (20) можно выделить функцию от e

,

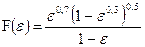график которой (рис.15.5) удобно использовать в расчетах проводимости отверстий при вязкостном режиме течения газов:

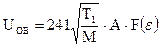. (21)

Так как отношение давлений заранее неизвестно, то расчет нужно вести методом последовательных приближений. В обычных вакуумных системах, работающих в стационарном режиме, чаще всего 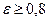. Это значение можно брать в качестве первого приближения.

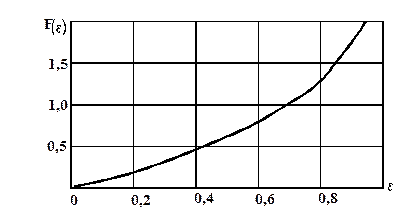
Рис.15.5 График F(e)

Молекулярный режим. В этом режиме поток через малую диафрагму из области Р₁ определяется количеством молекул, падающих на нее в единицу времени. Поскольку столкновения молекул между собой отсутствуют, то из области Р₂ в область Р₁ существует независимый поток газа. Суммарный поток – поток через отверстие в направлении будет G =G₁-G₂; где G₁ и G₂ – массовые потоки, проходящие через отверстие навстречу друг другу. Тогда проводимость отверстия в молекулярном режиме (U_­ом) рассчитывается по формуле

.

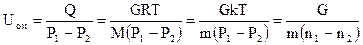Но 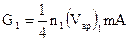; 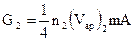. Тогда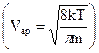

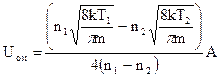. (22)

Если Т₁=Т₂=Т, то выражение (22) упрощается (M = mN_A):

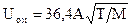, (23)

где М, кг/моль; А, м²; Т, К; U_ом, м³/с.

Молекулярно-вязкостный режим. Для этого течении можно пользоваться приближенной формулой

, (24)

где .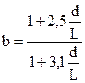

На границе с вязкостным режимом b=0,8, а на границе с молекулярным – 1,0. для приближенных расчетов можно принять b=0,9.

Поток через большую диафрагму. Большой диафрагмой называется отверстие, сравнимое с поперечными размерами сосуда, из которого выводится газ через это отверстие. На рис.15.6 показана схема соединения сосудов через большую диафрагму: в стенке толщиной Н имеется короткий трубопровод (например, фрезерование) и диафрагма, толщина которой h. Площадь трубопровода А_о, площадь диафрагмы А. Площади А_о и А малы по сравнению с поперечными размерами сосуда, но сравнимы между собой. Таким образом, отверстие с площадью А нужно рассматривать как большую диафрагму, приближаясь слева, и как малую диафрагму, приближаясь справа.

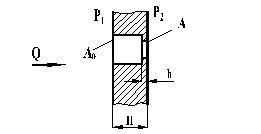
Рис. 15.6. Большая диафрагма

При течении газа слева направо общее сопротивление коммуникации, равное сумме сопротивлений ее последовательно соединенных элементов, будет

,

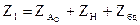Z_Ao – сопротивление отверстия А_о (как малой диафрагмы, Z_H - сопротивление канала в стенке, Z_бд – сопротивление большой (при течении газа от Р₁ к Р₂) диафрагмы.

При течении газа справа налево общее сопротивление будет

,

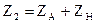где Z_A – сопротивление отверстии А как малой (при течении справа налево) диафрагмы.

Но как следует из электроаналогии, 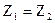, тогда , или .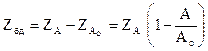

Так как , то

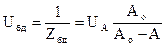. (25)

Выражение (25) для определения U_бд можно применять как при молекулярном, так и при вязкостном режимах течения.

Дата добавления: 2014-01-07