Методы наведения ракет. Метод пропорционального сближения

Метод пропорционального сближения ракеты с целью. Рассмотрим рис.4, на котором представлены текущие положения цели и ракеты, а также векторы их скоростей. Линию ракета-цель часто называют линией визирования. Введем неподвижную координатную ось ОО', относительно которой будем отсчитывать углы η и ζ. При использовании метода пропорционального сближения команда управления должна приводить к вращению вектора скорости ракеты с угловой скоростью, выражаемой соотношением

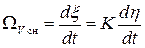, (4.2)

т.е. угловая скорость поворота вектора скорости ракеты должна быть пропорциональна угловой скорости вращения линии визирования. Коэффициент пропорциональности (навигационная постоянная) K > 1. Оптимальное значение K находится в пределах от 4 до 6. Если цель не маневрирует, то при управлении ракетой в соответствии с (4.2) .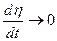

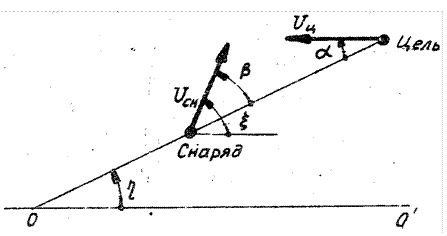
Рис.4. К описанию метода пропорционального сближения

Покажем справедливость данного утверждения. Для этого разложим скорости и ракеты на составляющие, параллельные линии визирования (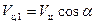, 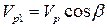) и перпендикулярные ей (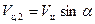,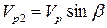). Сказанное иллюстрируется на рис.5. Здесь r - текущее расстояние между ракетой и целью.

Рис.5. Компоненты скоростей цели и ракеты

Как следует из рисунка 5, угловая скорость линии визирования, обязанная составляющим скоросте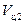й и 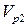, равна

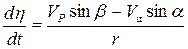. (4.3)

Если

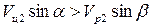, (4.4)

величина 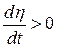(линия визирования поворачивается против часовой стрелки). Следовательно, в соответствии с (4.2) вектор скорости ракеты поворачивается в ту же сторону со скоростью 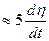. При этом угол β возрастает (рис.4), что приводит к уменьшению абсолютной величины разности 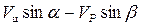, и, следовательно, к уменьшению угловой скорости .

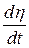Этот процесс продолжается до тех пор, пока неравенство (4.4) не преобразуется в равенство

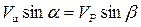. (4.5)

При этом 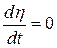. (4.6)

Отсутствие угловой скорости 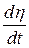означает, что линия визирования движется поступательно, а ракета и цель с составляющими скоросте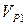й и 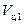(при встречных курсах) движутся к точке встречи. Если 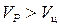, что обычно имеет место, то и при стрельбе вдогон, когда ракета и цель движутся в одну сторону (рис.6), встреча ракеты и цели обеспечена.

Рис.6. Положения скоростей V _Р1 и V _ц1 при стрельбе вдогон

Возвращаясь к рис.5, предположим, что в отличие от (4.4)

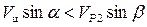. (4.7)

Тогда 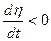(линия визирования поворачивается по часовой стрелке). Значит, вектор скорости ракеты тоже поворачивается по часовой стрелке. При этом угол β уменьшается. Вследствие этого абсолютная величина разности уменьшается до тех пор, пока неравенство (4.7) не превратиться в равенство (4.5) и .

Таким образом, в любом случае независимо от знака разности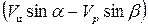

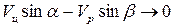, т.е.

при использовании правила (4.2).

Проведенное рассмотрение процесса наведения ракеты на неманеврирующую цель позволяет сделать следующие выводы:

- на начальном участке наведения ракета совершает маневр для достижения соотношения (4.5);

- в дальнейшем ракета движется почти прямолинейно в точку встречи. Прямолинейное движение ракеты выгодно как с точки зрения достижения максимальной дальности полета, так и для экономного расходования топлива. Сделанная оговорка о почти прямолинейном движении ракеты связана с необходимостью парирования атмосферных возмущений, воздействующих на ракету и цель, а также из-за погрешностей системы управления ракетой и маневра цели.

Указанные факторы могут привести к промаху ракеты. Промахом называется наименьшее расстояние между ракетой и целью. Если промах не превышает допустимой величины (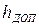), цель поражается полем осколков, образующихся при подрыве боевой части (боевого заряда) ракеты.

Найдем связь промаха с ошибкой определения угловой скорости линии визирования Ω. Для этого введем понятие минимальной дальности системы управления ракетой (мертвой зоны). Мертвая зона (r _min) - это расстояние между ракетой и целью, начиная с которого движение ракеты можно считать неуправляемым. Появление мертвой зоны связано с инерционностью системы управления, которую можно характеризовать временем запаздывания τ_з. Рассогласование, появившееся на входе системы за время τ_з до встречи ракеты с целью, не будет обработано.

Мертвую зону можно выразить как

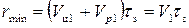. (4.8)

Предположим, что в какой-либо точке траектории ракеты при дальности до цели, равной τ_з, появляется ошибка измерения скорости линии визирования 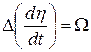, т.е. 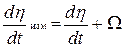. Это приводит к тому, что нулевое рассогласование в системе имеет место, когда 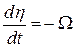. При этом в соответствии с (4.3) 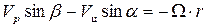или 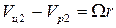. Если ошибка Ω появляется незадолго до подхода ракеты к мертвой зоне, то

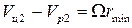. (4.9)

Считая с этого момента времени ракету неуправляемой, примем, что вектор скорости его не изменяет своей величины. Время, затрачиваемое на сближение с целью, равно

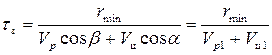, (4.10)

поскольку знаменатель (4.10) представляет собой скорость сближения ракеты и цели. В течение времени τ_з ракета и цель разойдутся на расстояние, равное промаху .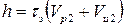

С учетом формул (4.9) и (4.10) получаем выражение для промаха

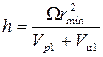. (4.11)

Из (4.11) можно определить промах при заданной величине Ω или допустимое значение Ω при заданных промахе и других величин в этой формуле.

Рассчитаем в качестве примера допустимое значение Ω_доп, если h_доп = 10 м, r_min = 1 км и скорость сближения 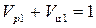км/с

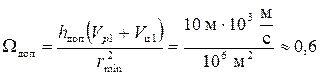град/с.

Если цель маневрирует, то для поддержания приближенного равенства 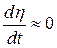ракета тоже должна маневрировать. При этом возможно некоторое увеличение промаха.

Лекция 17. ОСНОВЫ РАДИОУПРАВЛЕНИЯ. СПОСОБЫ УПРАВЛЕНИЯ

Дата добавления: 2014-01-07