
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ый достаточный признак
|
|
|
|
Пример
Исследовать на возрастание и убывание функцию 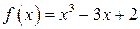 .
.
Решение.
Найдем производную 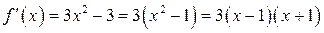 ,
, 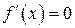 при
при 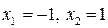 .
.
 |

 + – + у ¢
+ – + у ¢
 х
х


 –1 0 1 у
–1 0 1 у
Итак, функция 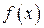 возрастает на промежутке
возрастает на промежутке 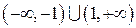 и убывает на промежутке
и убывает на промежутке 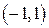 .
.
Пусть функция 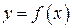 определена в некоторой окрестности точки
определена в некоторой окрестности точки 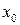 , включая и саму точку
, включая и саму точку 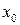 .
.
Определение. Функция 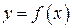 во внутренней точке области определения
во внутренней точке области определения 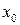 имеет локальный максимум (минимум), если найдется такая окрестность точки
имеет локальный максимум (минимум), если найдется такая окрестность точки 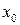 , в которой
, в которой 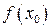 наибольшее (наименьшее) среди значений этой функции, т.е.
наибольшее (наименьшее) среди значений этой функции, т.е. 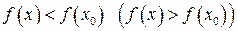 для всех х из указанной окрестности.
для всех х из указанной окрестности.
Точка 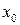 называется точкой максимума или минимума, а значение функции в этой точке максимумом или минимумом функции
называется точкой максимума или минимума, а значение функции в этой точке максимумом или минимумом функции 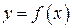 и обозначается:
и обозначается:
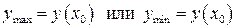 .
.
Термин «локальный» (относительный) экстремум обусловлен тем, что введенное понятие экстремума связано с окрестностью данной точки в области определения, а не со всей этой областью. В дальнейшем слово «локальный» будем для краткости опускать.
Необходимые условия экстремума.
 Теорема. Если функция
Теорема. Если функция 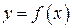 в точке
в точке 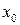 имеет локальный экстремум, то она в этой точке либо не дифференцируема, либо имеет в этой точке производную, равную нулю
имеет локальный экстремум, то она в этой точке либо не дифференцируема, либо имеет в этой точке производную, равную нулю 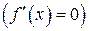 .
.
Точки, в которых производная равна нулю, называются стационарными.
Точки, в которых 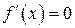 и точки, в которых функция не дифференцируема, называются критическими.
и точки, в которых функция не дифференцируема, называются критическими.
Достаточные условия экстремума.
 Теорема 1. Пусть для функции
Теорема 1. Пусть для функции 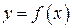 точка
точка 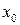 является критической и пусть функция
является критической и пусть функция 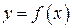 дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки 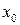 , исключая может быть точку
, исключая может быть точку  , в которой она непрерывна. Тогда, если при переходе через точку
, в которой она непрерывна. Тогда, если при переходе через точку 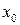 производная меняет знак, то функция в точке
производная меняет знак, то функция в точке 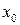 имеет локальный экстремум. Если при этом знак
имеет локальный экстремум. Если при этом знак 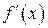 меняется с «+» на «–», то
меняется с «+» на «–», то 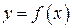 в точке
в точке 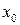 имеет локальный максимум; если же знак
имеет локальный максимум; если же знак 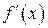 меняется с «–» на «+», то
меняется с «–» на «+», то 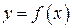 в точке
в точке 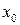 имеет локальный минимум.
имеет локальный минимум.
Пример. Исследовать на экстремум функцию 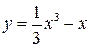 .
.
Решение: 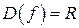 .
.
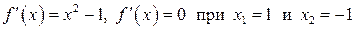 .
.
 |

 + – + у ¢
+ – + у ¢


 х
х
 –1 0 1 у
–1 0 1 у
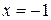 – точка максимума,
– точка максимума, 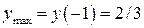 ,
,
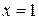 – точка минимума,
– точка минимума, 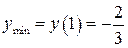 .
.
Вопрос 2. Исследование функций на выпуклость и вогнутость. Точки перегиба.
Пусть кривая задана уравнением 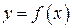 и пусть функция
и пусть функция 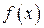 в точке
в точке 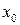 имеет конечную производную
имеет конечную производную 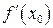 , т.е. в точке
, т.е. в точке 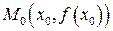 существует касательная к данной кривой, не параллельная оси оу (ибо угловой коэффициент ее конечен).
существует касательная к данной кривой, не параллельная оси оу (ибо угловой коэффициент ее конечен).


 у у М0
у у М0
 | |||||
 | |||||
 | |||||
 М0
М0
 |  | ||
0 
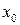
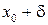 х 0
х 0 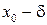
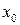
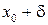 х
х
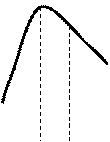
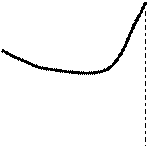
Определение. Будем говорить, что график функции 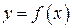 , дифференцируемой на интервале
, дифференцируемой на интервале 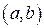 , является выпуклым (вогнутым), если график этой функции в пределах интервала
, является выпуклым (вогнутым), если график этой функции в пределах интервала 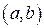 лежит не выше (не ниже) любой своей касательной.
лежит не выше (не ниже) любой своей касательной.

Теорема. Если функция 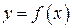 имеет на интервале
имеет на интервале 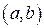 конечную вторую производную и если эта производная положительна
конечную вторую производную и если эта производная положительна 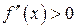 (отрицательна
(отрицательна 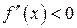 ) всюду на этом интервале, то кривая
) всюду на этом интервале, то кривая 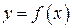 на интервале
на интервале 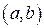 вогнута (кривая выпукла).
вогнута (кривая выпукла).
Пример. Найти участки выпуклости и вогнутости кривой 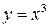 .
.
Решение. 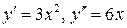 ,
,
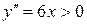 при
при 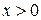 , значит, кривая вогнута на
, значит, кривая вогнута на 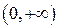 ,
,
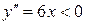 при
при 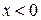 , значит, кривая выпукла на
, значит, кривая выпукла на 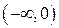 .
.
Определение. Точка 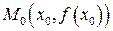 называется точкой перегиба кривой
называется точкой перегиба кривой 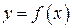 , если существует окрестность точки
, если существует окрестность точки 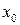 такая, что при
такая, что при 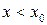 из этой окрестности выпуклость кривой направлена в одну сторону, а при
из этой окрестности выпуклость кривой направлена в одну сторону, а при 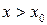 – в противоположную.
– в противоположную.
 Теорема (Необходимый признак точки перегиба).
Теорема (Необходимый признак точки перегиба).
Точка 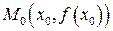 может быть точкой перегиба кривой
может быть точкой перегиба кривой 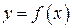 только если
только если 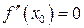 или
или 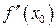 не существует.
не существует.
 Теорема (достаточный признак точки перегиба).
Теорема (достаточный признак точки перегиба).
Пусть функция 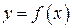 в некоторой окрестности точки
в некоторой окрестности точки 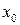 , за исключением, быть может, самой точки
, за исключением, быть может, самой точки 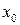 , имеет непрерывную вторую производную. Если
, имеет непрерывную вторую производную. Если 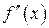 в точке
в точке 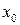 равна нулю или не существует и при переходе через точку
равна нулю или не существует и при переходе через точку 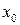 производная
производная 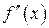 меняет свой знак, то точка
меняет свой знак, то точка 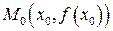 есть точка перегиба кривой
есть точка перегиба кривой 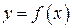 .
.
Пример. Найти точки перегиба кривой 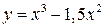 .
.
Решение: 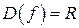 .
.
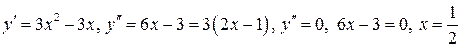 ;
; 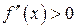 при
при 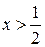 ,
, 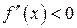 при
при 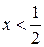 ,
, 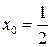 – абсцисса т.п., т.п.
– абсцисса т.п., т.п. 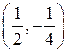 (сделать рисунок).
(сделать рисунок).
Вопрос 3. Асимптоты.
Определение. Прямая L называется асимптотой кривой 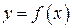 , если при удалении точки М кривой в бесконечность (т.е. расстояние этой точки от начала координат неограниченно возрастает) расстояние от этой точки до прямой L стремится к нулю. (Асимптоты бывают 3-х видов)
, если при удалении точки М кривой в бесконечность (т.е. расстояние этой точки от начала координат неограниченно возрастает) расстояние от этой точки до прямой L стремится к нулю. (Асимптоты бывают 3-х видов)
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 364; Нарушение авторских прав?; Мы поможем в написании вашей работы!