Неявные многошаговые методы Адамса

Неявный метод Адамса п -го порядка получается из общей разностной схемы линейных многошаговых методов при условии

р = n -2, а ₁ = а ₂ =… = а_{п- 2} = 0,

т. е.

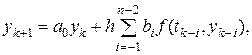
Здесь a ₀ ,b_{- 1}, b ₀ b ₁, b_{n -2} их всего и + 1, определяются из условий корректности полиномиальных решений п -го порядка.

Как и в явных методах Адамса § 23.1, а ₀ =1. Обозначим b_i = m _i (n), 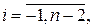подчеркивая тем самым зависимость значений коэффициентов b_i от порядка метода. Подставим выбранные значения параметров в условие корректности:

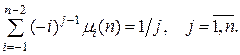
Относительно неизвестных коэффициентов m _i (n), 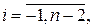получим систему из п линейных алгебраических уравнений:

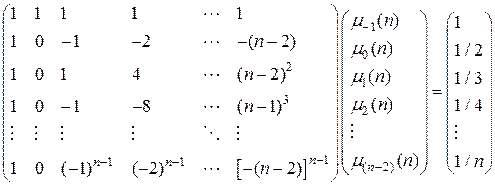
Решение этой системы однозначно определяет коэффициенты неявного метода Адамса п -го порядка.

Запишем неявные методы Адамса первого, второго и третьего порядков.

1. n = 1. Коэффициент m _-1 (1) = 1 и

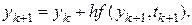
Разностная схема неявного метода Адамса первого порядка совпадает с неявным методом Эйлера.

2. п = 2. В этом случае

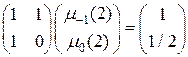
и искомые коэффициенты имеют следующие значения: . Неявный метод Адамса второго порядка

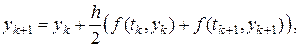
как легко видеть, является методом трапеций.

3. п = 3. Коэффициенты 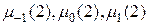вычисляются в этом случае из системы

Ее решение 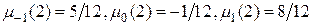. Неявный метод Адамса третьего порядка принимает вид:

Запись неявных методов Адамса более высоких порядков точности можно продолжить по аналогии.

Приведем теперь без вывода соотношение для расчета локальной погрешности неявного метода Адамса п -го порядка:

,

где значения коэффициента С_n для рассмотренных выше разностных схем соответственно равны: С ₁ = -1/2, С ₂ = -1/12, С ₃ = -1/24.

Сравнивая явные и неявные методы Адамса одного порядка между собой, можно отметить, что методы имеют одинаковую по порядку, но разную по знаку локальную погрешность.

Дата добавления: 2014-01-07