Упражнения. 1. Опираясь на геометрический смысл производной показать, что

1. Опираясь на геометрический смысл производной показать, что

а) производная функции для любого x равна 2;

б) производная функции 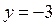для любого x равна 0;

в) производная функции 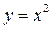для 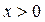положительна, а для отрицательна.

2. Уравнение движения точки по ее траектории (рис.3) имеет вид: 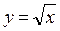. Показать, что точка тормозит при своем движении.

3. Функция – уравнение кривой спроса (рис.6). Показать, что для любых допустимых q производная этой функции отрицательна.

Производные основных элементарных функций. Таблица производных. Правила дифференцирования.

Опираясь на математическое определение производной (6), а также на ее физический (7) и геометрический (11) смысл, можно найти производные всех основных элементарных функций.

Пример 1. Пусть 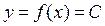(С – произвольная константа). Найдем производную 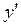этой функции. То есть найдем производную константы С.

Решение. Его можно получить тремя способами.

а) Способ 1 – геометрический.

Графиком функции 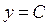является горизонтальная прямая. Касательной к этой прямой, проведенной в любой ее точке, будет она сама. Ее угол наклона 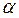к оси ох равен нулю. Но . Значит, согласно (11), .

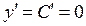б) Способ 2 – физический.

Функция 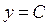от x не зависит, то есть с изменением x не меняется. А значит, скорость v (x) ее изменения равна нулю. Но ведь скорость изменения функции, согласно (7) – это производная функции. Таким образом, если 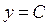, то 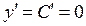. Физический смысл этого вывода очевиден: если координата y движущейся точки неизменна, то точка стоит. А значит, скорость ее движения равна нулю.

в) Способ 3 – математический.

Воспользуемся математическим определением (1.6) производной функции:

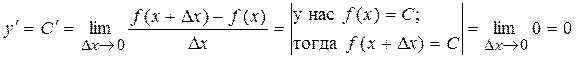
Итак, разными способами получаем один и тот же вывод: если 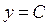, то .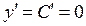

Пример 2. Пусть . Найдем производную 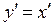этой функции.

Решение. Его наиболее просто получить геометрическим способом. Графиком функции является прямая, представляющая собой биссектрису первого и третьего координатных углов. Ее угол наклона к оси ох составляет 45º. Касательная к этой прямой в любой ее точке (при любом x) совпадает с этой же прямой. Поэтому, опираясь на геометрический смысл производной, получаем: . То есть 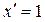. Этот же результат, заметим, следует и из математического определения производной (6):

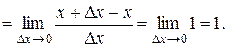
Пример 3. Пусть . Найдем производную 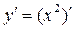этой функции.

Решение. Графиком функции 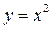является парабола. Касательная к ней в разных ее точках имеет разное направление (разный угол наклона 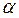к оси ох). Поэтому использовать геометрическую формулу (11) для нахождения производной этой функции в данном случае затруднительно. Затруднительно использовать и физический смысл производной (7). Тогда остается воспользоваться её математическим определением (6):

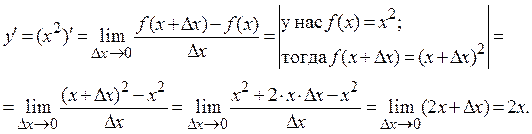
Итак, если 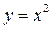, то .

Используя математическое определение производной (6), можно найти производные всех основных элементарных функций. Приведем уже в готовом виде таблицу производных этих функций.

Таблица производных основных элементарных функций

1. ;

2. ;

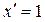3. ;

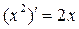4. ;

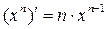5. ;

5^* ;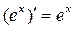

6. ;

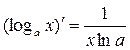6^*.;

7. ;

8. ;

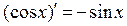9. ;

10. ;

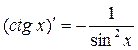11. ;

12. ; (17)

13. ;

14..

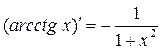Таблицу производных желательно выучить наизусть.

Выведем некоторые производные.

Пример 4. Производная функции , где n – целое положительное число, равна .

Решение. Имеем функцию . Воспользуемся для вывода математическим определением производной.

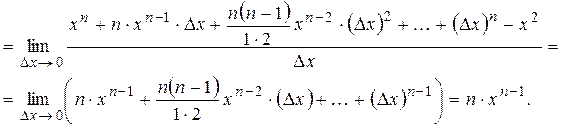
Что и требовалось получить.

Пример 5. Производная функции y=sinx, равна .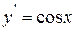

Решение.

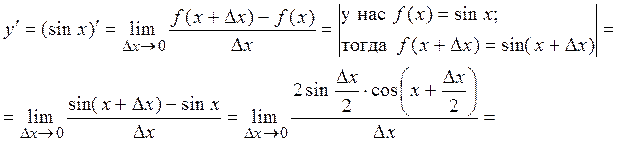
Пример 6. Производная функции равна .

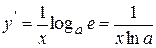Решение.

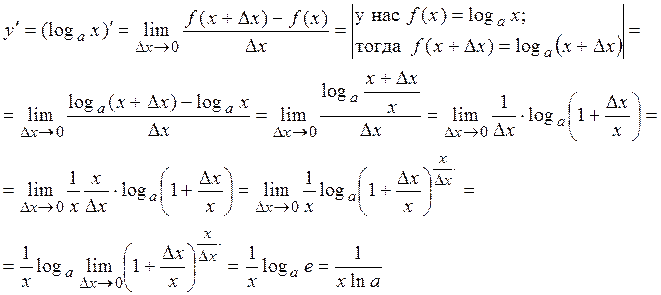
Обратим внимание, что производные степенной и показательной функции (формулы 4 и 5) находятся по разным формулам; что из всех показательных функций 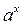наиболее простую производную имеет функция ; что из всех логарифмических функций наиболее простую производную имеет натуральный логарифм .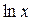

Нахождение производных многих других элементарных функций (более сложных, не входящих в эту таблицу) осуществляется на основе следующих правил вычисления производных (правил дифференцирования функций):

1. ;

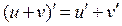2. ;

3. ;

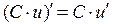4. ;

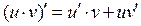5. 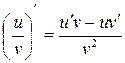. (18)

Здесь и – любые две дифференцируемые функции, а С – любая константа.

Несмотря на то, что таблица производных (17) и правила дифференцирования (18) известны еще из курса школьной математики, приведем вывод этих правил, основанный на использовании определения производной (6).

Теорема 10. Постоянный множитель можно вынести за знак, т.е. 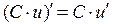, где С- константа.

Доказательство. Пусть у нас есть дифференцируемая функция 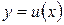. Найдем производную функции .

,

,

,

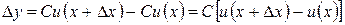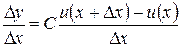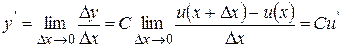, что и требовалось доказать.

Теорема 11. Производная суммы конечного числа дифференцируемых функций равна соответствующей сумме производных этих функций, т.е. .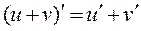

Доказательство. Пусть у нас есть две дифференцируемые функци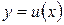и и . Найдем производную функции .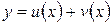

,

,

,

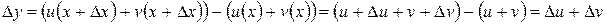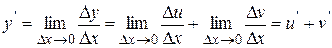, что и требовалось доказать.

Теорема 12. Производная от произведения двух дифференцируемых функций равна произведению производной первой функции на вторую функцию плюс произведение первой функции на производную второй функции т.е. .

Доказательство. Пусть у нас есть две дифференцируемые функци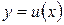и и . Найдем производную функции .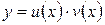

,

,

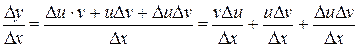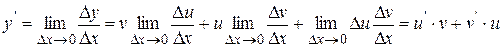, что и требовалось доказать.

Теорема 13. Производная дроби (т.е. частного от деления двух функций) равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя т.е. .

Доказательство. Пусть у нас есть две дифференцируемые функци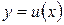и и . Найдем производную функции .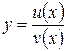

,

,

,

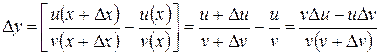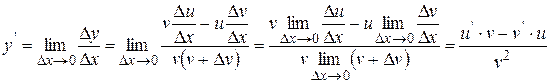, что и требовалось доказать.

Пример 7. ;

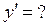
Решение.

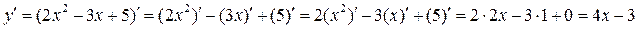
Пример 8. ;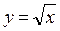

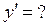
Решение.

.

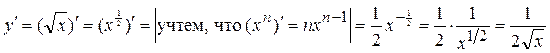Полученный результат

,

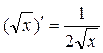наряду с формулами (17), полезно запомнить.

Пример 9. ;

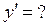
Решение.

.

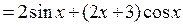Пример 10. ;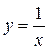

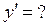
Решение.

Полученный результат

тоже полезно запомнить.

Дифференциал функции.

Понятие дифференциала функции тесно связано с понятием ее производной. Как и производная функции, дифференциал функции принадлежит к числу важнейших понятий математического анализа и введен в математику Ньютоном и Лейбницем параллельно с понятием производной.

Вспомним определение производной функции 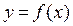в некоторой фиксированной точке x (формулы 5 и 6):

(19)

Здесь 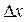– приращение аргумента x, а 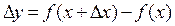– соответствующее приращение функции y.

Будем считать, что данная функция 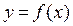дифференцируема в рассматриваемой фиксированной точке x. То есть будем считать, что производная 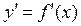в этой точке существует и конечна. Тогда, согласно (19),

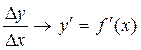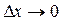при (20)

А это значит, что при малых значениях 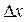будем иметь:

(21)

Причем приближенные равенства (21) будут тем точнее, чем меньше 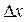(и соответственно чем меньше ).

А теперь будем считать приращение 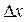аргумента функции 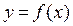не просто малым, а бесконечно малым, и назовем его дифференциалом аргумента x. Введем (следуя Лейбницу) для него и специальное обозначение:

dx – дифференциал аргумента x. (22)

Таким образом, дифференциал dx аргумента x – это бесконечно малое приращение 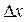этого аргумента. Конечно, только что введенное понятие дифференциала переменной x – математическая абстракция (она сродни диаметру точки или толщине линии). Но математика постоянно пользуется абстракциями, поэтому еще одна абстракция пугать нас не должна.

Если приращение 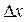аргумента x бесконечно мало (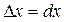), то и приращение функции y тоже будет бесконечно мало. Обозначим его символом dy и будем называть дифференциалом функции y. Так как 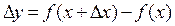, то

– дифференциал функции y. (23)

Если теперь в приближенных равенствах (21) заменить малые, но конечные 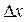и на бесконечно малые dx и dy, то эти равенства станут точными.

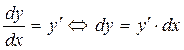(24)

Оба равенства (24) имеют важный смысл. Первое из них дает выражение производной 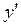функции y через отношение дифференциалов dy и dx функции и аргумента. А второе дает выражение дифференциала функции dy через производную функции 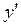и дифференциал аргумента dx.

Кстати, если учесть, что 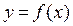, то последнее равенство (24) можно записать подробнее:

(25)

А если еще учесть исходное выражение (23) для дифференциала 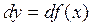функции 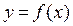, то из последнего равенства получаем:

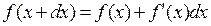(26)

Равенство (26) позволяет записать значение функции 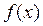в точке 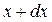, бесконечно близкой к точке x, через значение функции и ее производной в самой точке x. Эта формула имеет большое теоретическое значение.

Если в равенстве (26) заменить бесконечно малое dx на малое, но конечное 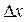, то вместо точного оно станет приближенным:

(27)

Равенство (27) называется простейшим вариантом формулы Тейлора. Эта приближенная формула тем точнее, чем меньше 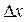. Она используется для приближенного вычисления значения по значениям 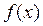и . У формулы (27) имеется и ясный геометрический смысл – мы его укажем далее. Там же мы приведем и полный вариант формулы Тейлора.

В частности, применяя эту формулу для функций ; ; 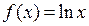; 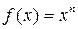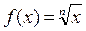, и т.д., получим следующие интересные формулы для производства приближенных вычислений:

1) ; (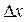– в радианах) 2) ; (28)

3) ; ;

4) ; ;

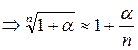В частности, используя последнюю формулу, получим:

.

Для сравнения: точное значение 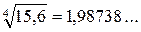. То есть приближенное значение 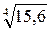, полученное вручную, отличается от его точного значения лишь в четвертом знаке после запятой.

Вернемся все же к формулам, служащим для нахождения дифференциала функции 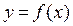. На базе этих формул можно установить следующие

свойства дифференциала функции:

1.

2.

3.

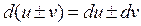
4.

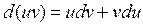
5. 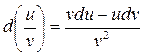(29)

Здесь С – любая константа, а 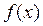, и – любые дифференцируемые функции. Действительно:

1. ;

2. .

Совершенно аналогично доказываются и остальные свойства (29).

Дата добавления: 2014-01-07