Мультиплетность. Эффекты окружения ядрами

Правила аддитивности для химических сдвигов.

Для химических сдвигов применимы правила аддитивности вкладов отдельных частей молекулы или заместителей по формуле:

i

d = d_ст + SD_i,

d_ст – стандартное значение химического сдвига для определенных частей молекул, D_i – вклад отдельного заместителя.

5.1. Природа явления.

В случае сжиженного фтористого водорода HF, в котором оба ядра магнитны (I = ½), в тефлоновой ампуле имеет место взаимодействие магнитных ядер через связевые электроны, которые тоже магнитные частицы, ибо для них I = ½:

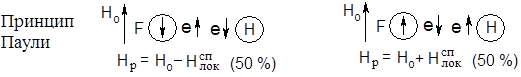
Практически половина ядер фтора ориентирована по полю, половина – против поля, эти ядра благодаря принципу Паули свою ориентацию передают на ближний к протону электрон, который благодаря своей прецессии создает на каждой половине ядер протона свое локальное спиновое магнитное поле (Н^сп_лок). Таким образом, в спектре ПМР HF появляется два сигнала равной интенсивности (50%:50%=1:1), расстояние между которыми называют константой спин-спинового взаимодействия J, имеющую размерность частоты в Гц (и только в Гц)..

Группа магнитных ядер, взаимодействующих между собой через связевые электроны, называется спиновой системой магнитных ядер. Сила взаимодействия меду ядрами в этой системе и характеризуется константой спин-спинового взаимодействия, которая обозначается латинской буквой J (дзей) с индексами внизу и вверху, например, для системы HF – ¹J_HF. Индекс справа внизу указывает взаимодействующие ядра, индекс вверху слева указывает на количество простых связей, связывающих взаимодействующие ядра.

5.2. Факторы, определяющие константу спин-спинового взаимодействия.

Прежде всего необходимо отметить, что J является внутренней характеристикой спиновой системы, определяется ее строением, и не зависит от такого внешнего фактора, как напряженность постоянного магнитного поля

Н₀. Константа J зависит от трех факторов: а) природы взаимодействующих ядер; б) числа и типа химических связей, разделяющих эти ядра;

в) пространственного строения молекул, в которые спиновая система входит:

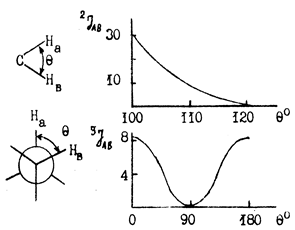Система J, Гц

Н-F 650

H-P 300

H-H 40

H-C-H 20

H-C-C-H 12

H-C-C-C-H 0,2(dn =0,1Гц)

H-C-C=C-H 3

Через четыре простых

σ-связей спин-спиновое

взаимодействие не передается.

Такая зависимость констант J от пространственного строения молекул используется в химии для конформационных исследований и конформационного анализа.

5.3 Спектры І-го и ІІ-го порядков.

Спиновая система магнитных ядер одной природы (например, протонов) обозначается буквами латинского алфавита, первой и одной из последних, т.е. АХ, если соотношение Δν_AХ/J_АХ > 6 (cистема І-го порядка), или двумя соседними буквами, т.е. АВ, если соотношение Δν_AВ/J_АВ < 6 (cистема ІІ -го порядка). Здесь Δν_AХ (разница химических сдвигов взаимодействующих ядер в Гц), поскольку J_АХ измеряется только в Гц.

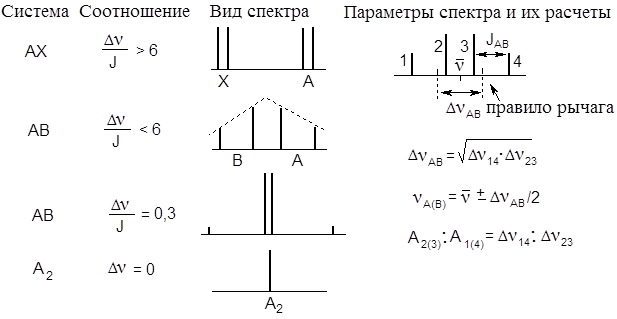
Вид спектра спиновой системы зависит от соотношения Δν/J. Возьмем для примера 4 ситуации:

В спектре ІІ-го порядка происходит искажение мультиплетов: чем меньше соотношение Δν/J, тем сильнее расходятся линии, тем интенсивнее становятся сближающиеся линии 2 и 3 и тем больше понижаются интенсивности крайних, расходящихся линий (как бы под крышу, показанную на схеме пунктирными линиями). Более того, появляется множество дополнительных линий. Расшифровать такой спектр, в отличие от спектра І-го порядка, без ЭВМ невозможно. Поэтому химики работают в основном со спектрами І-го порядка.

Когда Δν = 0 (например, соединение ClCH₂Cl), центральные линии сливаются в одну, а крайние исчезают, т.е. спектр превращается в одну линию, которую называют синглетом. Если 2 линии в мультиплете – это дублет, 3 – триплет, 4 – квадруплет, 5 –квинтет, 6 – секстет. Для вещества CH₃Cl наблюдается только одна линия – синглет (Δν = 0).

Если на приборе с рабочей частотой 60 МГц величина Δν/J = 1 (спектр ІІ-го порядка), то на современном приборе на 600 МГц Δν/J = 10, т.е. это уже спектр І-го порядка. Преимущество современного прибора очевидно.

5.4. Графический метод построения спектров спиновых систем.

5.4.1. Спектр системы АХ.

Построим для примера ПМР спектр вещества дихлоруксусного альдегида CHCl₂-COH, в котором имеется спиновая система АХ. Для этого вещества находим величины d: d_СНО = 9,6 (см. табл. 1.4 пособия [1]), рассчитываем d_СН по табл. 1.1 того же пособия, т.е. d_СН = 1,55 + 1,05 + 2×2,55 = 7,7 м.д., Dd_АХ = 9,6 – 7,7 = 1,9 м.д.

Предположим, что спектр наблюдают на приборе с n_о = 60 МГц, тогда 1м.д.= Dn_АХ×10⁶/n_о = Dn_АХ×10⁶/60×10⁶ Гц = Dn_АХ/60 Гц. Отсюда: Dn_АХ = 60 Гц, т.е. 1м.д. соответствует 60 Гц, а 1,9м.д. – 114 Гц. Допустим, для этой системы J_АХ = 12 Гц (обычно меньше для подобных систем, см. табл. 1.7 метод. пособия [1]), тогда Dn_АХ/ J_АХ = 114Гц/12Гц = 9,5 > 6.

Таким образом, спектр рассматриваемой спиновой системы является спектром І-го порядка. Такой спектр легко расшифровывается и его в свою очередь легко построить на бумаге. Для этого надо принять определенный масштаб, например 1Гц соответствует расстоянию в 1мм. Тогда расстояние между линиями спектра равняется 114 мм, а интегральная интенсивность линий определяется по формуле А = 2ⁿ, где n – число соседних атомов водорода, а 2 – две ориентации магнитного дипольного момента ядра (по полю Н₀ и против поля). Для спиновой системы АХ каждый протон имеет одного соседа, поэтому интегральные интенсивности для них А_А=А_Х=2¹= 2. Спектр имеет вид:

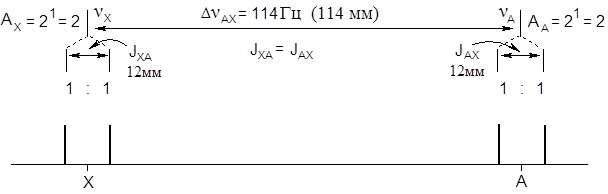
Внизу диаграммы изображен спектр ПМР системы АХ с масштабом интенсивности сигнала: 1 единица интенсивности – 10 мм.

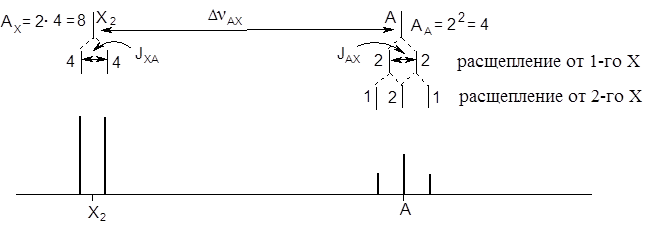
5.4.2. Спектр системы АХ₂.

Внизу диаграммы изображен спектр ПМР системы АХ₂ с масштабом интенсивности сигнала: 1 единица интенсивности – 5 мм. Как видно, в этом спектре, как и в предыдущем, наблюдается также два мультиплета (наименьшее число мультиплетов в любой системе), но вместо двух дублетов имеется один дублет и один триплет, в котором центральные сигналы складываются при повторном расщеплении. Количество сигналов, т.е число полос N в мультиплете в общем случае для всех ядер спиновой системы, состоящей только из двух типов ядер, определяется по формуле: N = 2In_c + 1, где I – спиновое квантовое число соседних магнитных ядер, n_c – их количество.

В случае спектров ПМР для спиновых систем, состоящих из двух неэквивалентных групп ядер водорода, когда I = ½, число полос в мультиплете определяется соотношением: N = n_c + 1, т.е. число полос на одну больше числа соседних атомов водорода. Поэтому для спиновой системы АХ₂ для протонов А наблюдается триплет (два соседних атома Х), для протонов Х – дублет (один соседний атом А). То же количество сигналов автоматически получается и графическим методом.

Следует также заметить, что если соседняя группа не содержит магнитных ядер (например, -СО- или -СО-О-), то, согласно формуле, N = 1, т.е. наблюдается синглет для любой группы, содержащей эквивалентные водороды (СН₃, СН₂ или СН).

Для объяснения количества сигналов в мультиплете и соотношения их интенсивностей воспользуемся физической сущностью явления, т.е. значением реальной напряженности магнитного поля Н_р, являющегося суммой напряженности Н₀ и локального поля Н^сп_лок, создаваемого соседними магнитными ядрами:

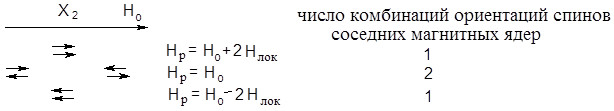
Как видим, протоны находятся в трех разных магнитных полях (3 сигнала), создаваемых 4-ма комбинациями ориентаций спинов соседних протонов, две из которых эквивалентны, вследствие чего и наблюдается следующее соотношение интенсивностей этих сигналов (1: 2: 1).

Соотношение интенсивностей сигналов в мультиплете, как и их количество, можно, не прибегая к методу графического построения спектра, также определить по треугольнику (косынке) Паскаля:

n_с: сигналы при I = ½ сигналы при I = 1

0 1 1

1 1 1 1 1 1

2 1 2 1 1 2 3 2 1

3 1 3 3 1 1 3 6 7 6 3 1

4 1 4 6 4 1 1 4 10 16 19 16 10 4 1

5 1 5 10 10 5 1

6 1 6 15 20 15 6 1

5.4.3. Спектр системы АМХ.

Эта спиновая система дает спектр I=го порядка и состоит из трех неэквивалентных ядер. Проводим построение ее спектра:

Все проявляющиеся в спектре константы спин-спинового взаимодействия в данном случае взяты неодинаковыми: J_АХ ¹ J_АM ¹ J_MХ ¹ J_АХ. Благодаря этому в спектре имеется три квадруплета с линиями одинаковой интенсивности. В реальном спектре величины констант спин-спинового взаимодействия находят как расстояния в Гц и между соседними линиями, и через одну линию, как это показано на схеме.

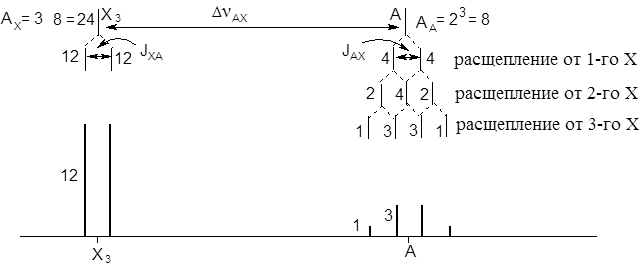5.4.3. Спектр системы АХ₃.

Строим спектр системы тем же графическим методом:

Физическая сущность явления:

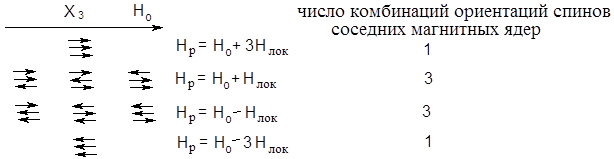
5.4.4. Спиновая система А_NM_ZХ_Y.

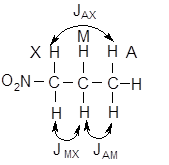Для примера возьмем спиновую систему молекулы 1-нитропропана и рассмотрим спин-спиновые взаимодействия в ней:

Спин-спиновое взаимодействие через 4 s-связи J_AX = 0, учитываются лишь спин-спиновое взаимодействие через 3 s-связи, ибо они не равны 0. Тогда количество полос в мультиплете протонов М будет зависеть от того, равны или не равны между собой константы J_AМ и J_МX. Число полос в мультиплетах протонов А и Х от этого зависеть не будет:

J_AМ ¹ J_МX J_AМ = J_МX

Протоны Число полос Протоны Число полос

А Z + 1 A Z + 1

М (N + 1)(Y + 1) M N + Y + 1

Х Z + 1 X Z + 1

Дата добавления: 2014-01-07