Лекция 5. Модели отказов

При оценке и прогнозировании надежности ЛК, как и всех ТС, применяют модели отказов - математическое описание процесса формирования закона наработок до отказа (сроков службы).

Модели отказов могут быть двух основных видов - статистические и физико-вероятностные, в зависимости от той информации, которая используется для получения закона.

При решении задач надежности источниками статистической информации для получения эмпирической функции, оценивающей закон распределения наработок до отказа (сроков службы), например в виде гистограммы, служат или специально проводимые испытания, или наблюдения и обработка данных об отказах изделий в процессе эксплуатации.

По полученной гистограмме, которая является экспериментальной оценкой плотности вероятности, при необходимости может быть подобран теоретический закон распределения (рис. 5.1).

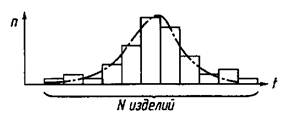
Рис. 5.1

С точки зрения характера априорных сведений о функции распределения обычно рассматривают два основных случая.

1. Вид функции распределения известен априори, например, из результатов статистических исследований аналогичных изделий или прототипа. В этом случае задача статистической обработки заключается в определении числовых параметров полученного распределения.

2. Вид функции распределения неизвестен или известен лишь предположительно. В этом случае на основании анализа статистического материала принимается гипотеза о виде функции распределения, а для получения необходимых данных выполняются процедуры, которые содержат следующие этапы:

— построение вариационного ряда;

— построение гистограммы;

— принятие гипотезы о виде функции распределения;

— оценка точечных значений параметра для функции распределения предполагаемого типа;

— проверка непротиворечия экспериментальных данных принятой гипотезе о функции распределения.

Полученный в результате обработки статистической информации закон распределения наработок ЛК до отказа, выраженный в дифференциальной форме в виде плотности вероятности или в интегральной форме в виде функции распределения, является полной характеристикой надежности. Он позволяет определить вероятность безотказной работы Р(t) для любого заданного значения t = Т‚ а также средний срок службы или среднюю наработку до отказа. Для получения экспериментальных данных, позволяющих судить о законе распределения, требуется, как правило, очень длительное время, так как фиксируется конечная стадия процесса изменения работоспособности изделия - его отказ. Для сложных изделий, когда для испытания можно выделить один или небольшое количество образцов, а изделие обладает высоким уровнем надежности, получение необходимого объема статистических данных практически невозможно.

Возможности получения достаточной информации при стендовых испытаниях также встречаются в машиностроении достаточно редко и могут иметь место лишь при испытании стандартных и унифицированных узлов (например, подшипников качения). Более полная информация о действительном законе распределения сроков службы отдельных элементов может быть получена из сферы ремонта машины. для этого необходимо, чтобы при производстве ремонтных работ оценивалась степень повреждения (например, износа) основных деталей и по этим данным определялась скорость процесса потери изделием работоспособности.

Схема получения информации о надежности данного элемента из сферы эксплуатации и ремонта показана на рис. 5.2, где 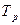- период до очередного планового ремонта. Дополнительный объем статистической информации о надежности изделия можно получить также, если использовать специфику возникновения параметрического отказа.

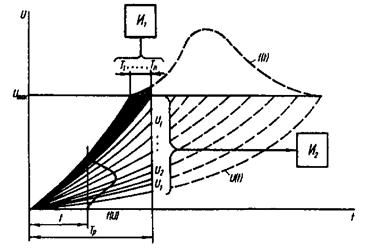
Рис. 5.2. Источник статистической информации при эксплуатаци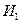и () и

ремонте ().

Эта специфика заключается в том, что при стендовых испытаниях можно назначить более строгий допуск на выходной параметр и этим ускорить время наступления параметрического отказа. Однако для этого потребуется, во-первых, применение более чувствительной измерительной аппаратуры и, во-вторых, осуществление коррекции полученной информации для оценки действительных наработок (сроков службы) до отказа. Последнее опирается на методы прогнозирования изменения выходных параметров за пределами значений, полученных из эксперимента. При построении моделей отказов на основе статистической информации данные о законе надежности могут быть получены:

1. На основании длительных стендовых или эксплуатационных испытаний получают объем статистических данных, достаточный для оценки эмпирической функции распределения наработок (сроков службы) до отказа. Это возможно, как правило, лишь для ограниченного числа изделий, которые имеют стабильную конструкцию и производятся большими партиями. Типичным примером являются подшипники качения.

2. Из эксперимента получают сведения лишь о тех отказах, которые произошли за период испытания. В этом случае суждение о надежности изделия за пределами данного периода либо недопустимо, либо требует привлечения дополнительной информации.

3. При стендовых испытаниях получают информацию о параметрических отказах при более строгих допусках к выходным параметрам. Ее может быть достаточно для выявления закона надежности, но требуется осуществить пересчет на нормальные условия эксплуатации.

4. Статистическая информация, которая получена при эксплуатационных испытаниях, дополняется информацией из сферы ремонта. Для получения закона надежности необходимо применить процедуру прогнозирования процесса потери изделием работоспособности (см. рис. 5.2).

На основе анализа построенной гистограммы (рис. 5.1) по статистической информации выбирается теоретический закон распределения наработок до отказа (сроков службы). Основные теоретические законы распределения наработок до отказа (сроков службы) приведены в табл. 5.1.

Таблица 5.1

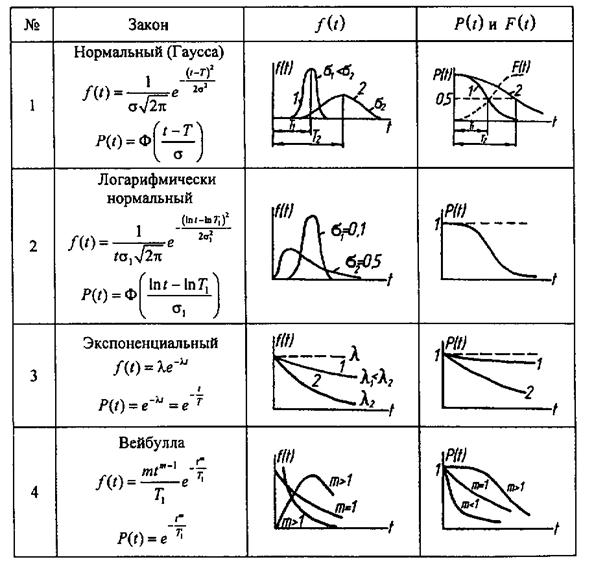
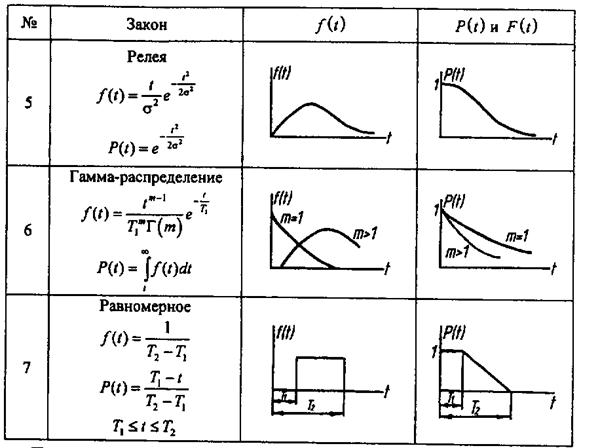
В практике расчета надежности наиболее часто используются нормальное распределение (распределение Гаусса), экспоненциальное и равномерное.

Нормальное распределение (распределение Гаусса) широко используется во многих областях науки и техники. Это двухпараметрическое симметричное распределение, числовыми характеристиками которого являются 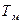- математическое ожидание и 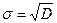- среднее квадратическое отклонение данной случайной величины.

В практике определения вероятности безотказной работы Р(t) применяют табулированную функцию нормального распределения (функцию Лапласа) в виде

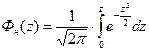при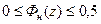

или ту же функцию при ,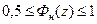

где .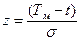

Пользуясь таблицами для нормированной 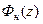или общей функции Лапласа, можно рассчитать вероятность безотказной работы как

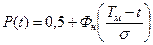или .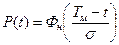

Если вероятность безотказной работы задана и требуется определить время t = Т‚ при котором обеспечивается данное значение Р(t) ‚ то пользуются таблицами квантилей нормального распределения.

Нормальный закон в ряде случаев рекомендуют применять при постепенных отказах, особенно тогда, когда начальное значение параметра имеет большую дисперсию, а его изменение во времени протекает достаточно стабильно.

Экспоненциальное распределение. Экспоненциальный закон является однопараметрическим, удобным для расчетов надежности, особенно для сложных расчлененных систем, если известна средняя наработка до отказа.

Экспоненциальное распределение хорошо описывает случай, когда вероятность отказа не зависит от длительности предыдущего использования изделия, т.е. когда возникают в основном внезапные, а не постепенные отказы.

Равномерное распределение. При данном распределении все отказы совершаются за отрезок времени от 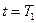до 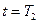, и вероятность их появления одинакова для любых одинаковых промежутков времени внутри данного отрезка.

Равномерное распределение может заменить экспоненциальное при 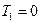и значениях Р(t)>0,9 (линеаризация экспоненты).

Основная трудность при расчете показателей надежности с использованием рассмотренных выше моделей отказов заключается в том, чтобы выбрать такое теоретическое распределение, которое с наибольшей степенью достоверности отражало бы процессы, приводящие к отказам ТС.

При анализе надежности ТС, когда за рассматриваемый промежуток времени эксплуатации или испытаний проявляются все учитываемые виды отказов, и полученные статистические данные являются репрезентативной выборкой генеральной совокупности, обычно оценивается параметр сложного потока отказов 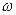, как сумма параметров потоков его составляющих 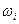, т.е.

.

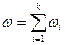Этот принцип используют при анализе отказов различных элементов и подсистем сложных ТС. Например, рассматривая поток отказов ТС, его разбивают на потоки отказов механических, гидравлических, электромеханических и электронных систем. В других случаях разделяют ТС на функциональные системы и узлы и оценивают удельный вес отдельных составляющих потока отказов. Для более детального анализа характера и причин отказов строят так называемое «дерево отказов» (схема Исикава) (рис. 5.3а) или диаграмму, характеризующую удельный вес различных отказов изделия (диаграмма Парето). Так, например, при анализе отказов объемного регулируемого гидропривода строится «дерево отказов», в котором отражаются слабые элементы гидропривода: уплотнения 1, золотниковые распределительные устройства 2, механические 3 и электрические 4 элементы, клапаны 5 и фильтры 6.

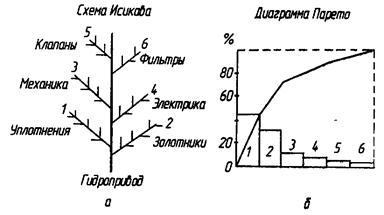
Рис. 5.3. Графический анализ потока отказов: дерево отказов (а) (схема Исикава)

и диаграмма Парето (б).

На ответвлениях слабых элементов указываются виды и причины отказов, например, «износ уплотнений», «засорение фильтра», «повышение усилия страгивания золотника» и др.

В диаграмме Парето (рис. 5.3б) указывается процентное соотношение рассматриваемых отказов, которые ранжируются по значимости. и строится кривая кумулятивного (накопленного) процента отказов.

При оценке надежности сложных ТС в общем случае параметр потока отказов 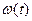является функцией времени. Он зависит от того отрезка времени t = Т, для которого определяется параметр потока отказов ω. Если значение 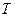меньше математического ожидания 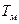, то на значении ω будут сказываться особенности закона 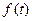. Если же рассматриваются такие отрезки времени, когда произошло значительное число отказов, т.е. 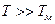, то происходит стабилизация ω и его можно принять постоянной величиной (ω=const.).

Если же распределение сроков службы до отказа 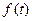подчиняется экспоненциальному закону, то поток отказов сразу является стационарным, а интенсивность отказов совпадает с параметром потока отказов .

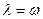Показатель «параметр потока отказов» применяют для оценки надежности ТС как при отказах функционирования, так и при параметрических отказах.

При отказах функционирования рассматривают либо опытный образец ТС, либо оценивают такие отказы, которые легко устранимы в процессе эксплуатации и не сказываются на производительности ТС.

Характерным примером модели возникновения внезапных отказов может служить модель надежности механических систем, когда причиной отказа является разрушение конструкции из-за экстремальных ситуаций. К этой категории относится модель «нагрузка - прочность», учитывающая рассеивание прочностных характеристик материалов и действующих нагрузок.

Простейшая модель «нагрузка - прочность» представлена без фактора времени на рис. 5.4.

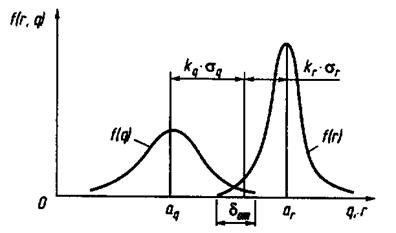
Рис. 5.4. Модель возникновения внезапного отказа (модель «нагрузка - прочность»).

Вероятность безотказной работы Р при однократном нагружении определяется из условия, что нагрузки не превзойдут требуемых показателей прочности.

Если распределения величин r (нагрузка) и q (прочность) подчиняются нормальному закону (что, однако, не всегда соблюдается) то вероятность неразрушения конструкции определяют по зависимости:

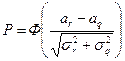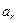, где и 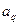- математические ожидания нагрузки и прочност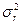и;

и 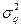- среднеквадратические отклонения нагрузки и прочности.

Физико-вероятностные модели отказов. Эти модели используются при прогнозировании параметрической надежности ТС в случае изменения (деградации) выходногопараметра Х во времени, обусловленного процессами старения материала деталей, износа поверхности деталей, коррозии и других необратимых процессов. Отказ возникает при достижении параметром своего предельно допустимого значения 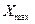‚ что произойдет через некоторый случайный промежуток времени работы изделия t = Т.

На схеме рис. 5.5 показаны основные этапы формирования закона распределения 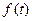. При 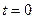имеет место рассеивание начальных параметров изделия 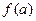относительно своего математического ожидания 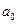. Это связано с дисперсией показателей новой машины, с возможностью работы машины при различных режимах и с протеканием таких процессов, как вибрация. деформации и др., которые проявляются сразу же при функционировании машины. Затем на ухудшение параметров изделия в процессе эксплуатации сказываются медленно протекающие процессы старения (износа и др.). В общем случае процесс изменения параметра может начаться через некоторый промежуток времени 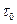‚ который является случайной величиной и связан с накоплением повреждений.

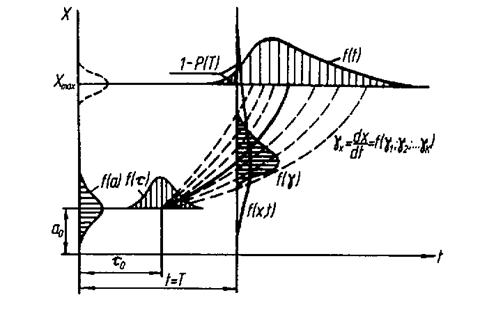
Рис. 5.5. Общая схема формирования параметрического отказа.

Процесс изменения параметра со скоростью 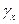, также является случайным и зависит от интенсивности изменения характеристик отдельных элементов изделия. В результате всех этих явлений происходит формирование закона распределения 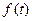, который определяет вероятность выхода параметра за границу 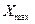, т.е. вероятность отказа 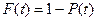. Следует отметить, что в общем случае значение 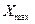также может иметь рассеивание, если оно оценивает диапазон требований потребителя к предельным значениям показателей машины. Данная схема в общем виде описывает процесс возникновения отказа и при частных значениях входящих параметров может отражать те или иные случаи, характерные для определенных условий работы и конструктивных особенностей изделия.

Если процесс изменения параметра начинается сразу (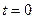), то получаем типичную схему возникновения постепенного параметрического отказа. Если при достижении 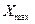будет иметь место резкое возрастание 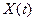, то, как правило, возникнет отказ функционирования.

Дата добавления: 2014-01-07