Линейная модель параметрического отказа

В практике расчетов, при прогнозировании параметрической надежности, весьма часто используется линейная модель параметрического отказа, когда рассеивание выходного параметра подчиняется нормальному распределению, а его изменение во времени - линейному закону (рис. 5.6.),

т.е.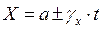

где: - начальное значение параметра ; 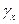- скорость изменения параметра при эксплуатации изделия.

Рис. 5.6. Линейная модель параметрического отказа.

Из этой формулы следует, что наработка (срок службы) до отказа, который определяет время t = Т достижения параметром значения 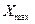будет:

Значение Т является функцией двух случайных аргументов и 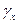, которые при нормальном законе распределения характеризуются математическим ожиданием (соответственно и 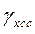) и средним квадратическим отклонением (и ). В этом случае для каждого фиксиро­ванного значения t = Т параметр X также будет распределен по нормальному закону 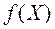с характеристиками:

математическое ожидание -

среднее квадратичное отклонение -

В этой модели нормальному распределе­нию подчиняются начальное значение параметра и скорость процесса 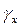, т.е. разные по размерности величины.

Оценивается именно скорость процесса, потому что она зависит от большого числа факторов, характеризующих режимы и условия работы изделия и не связанных с длительностью его эксплуатации. Если рас­сеивание данной величины является результатом суммирования от воз­действия ряда независимых случайных факторов, сравнимых по своему значению, то согласно центральной предельной теореме теории вероятностей результирующее распределение будет приближаться к нормальному.

Полученные зависимости для 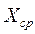и определяют область состояний параметра X в функции времени t и позволяют получить характе­ристики параметрической надежности ТС.

Вероятность отказа определяется вероятностью выхода пара­метра X за пределы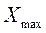(площадь под кривой 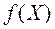, отсекаемая гра­ницей области работоспособности 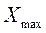, а вероятность безотказной работы 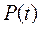численно равна площади под кривой 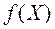, находящейся в области работоспособности. Поскольку площадь под кривой нормального распределения может быть подсчитана с помощью функции Лапласа Ф(X) при 0,5 < Ф < 1, получим:

.

Закон надежности не подчиняется в данном случае нормальному распределению, он асимметричен, находится в области положительных значений t, а показатель 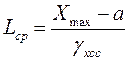является его медианой.

Эти формулы используются для оценки надежности ТС, в том числе и для ЛК, на стадии проектирования или для новой машины до начала ее эксплуатации. Для расчета необходимо определить следующие величины:

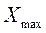- предельно допустимое значение выходного параметра, которое устанавливается техническими требованиями к ТС (на основании стандартов, нормативов, требований заказчика);

и - характеристики распределений начальных параметров ТС, которые зависят от точности (качества) изготовления и от возможного их изменения при действии сил, температур, параметров окружающей среды и других факторов, связанных с работой ТС. Допустимые значения этих показателей также должны быть установлены техническими требованиями. При наличии опытного образца или новой машины они могут быть определены экспериментально;

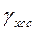и - характеристики скорости процесса изменения выходных параметров изделия в результате его старения (износа). Их оценка связана с использованием закономерностей, описывающих физику процесса старения и с расчетом того влияния, которое оказывает данный процесс на выходные параметры.

Эти расчеты являются ключевыми для возможности прогнозирования характеристик надежности на ранних стадиях создания машины.

Дата добавления: 2014-01-07