Принятие решений в условиях риска. Обычно основывается на одном из следующих критериев:

Обычно основывается на одном из следующих критериев:

1) ожидаемого значения (прибыли или расходов);

2) комбинации ожидаемого значения и дисперсии;

3) известного предельного уровня;

4) наиболее вероятного события в будущем.

Рассмотрим каждый из этих критериев.

• Критерий ожидаемого значения.

Использование критерия ожидаемого значения, обусловленное стремлением максимизировать ожидаемую прибыль (или минимизировать ожидаемые затраты), представляет собой естественный переход от условий полной определенности. Количественно этот критерий можно выразить в денежных единицах или в единицах полезности денег.

Для пояснения разницы между непосредственно деньгами и их полезностью предположим, что инвестиции в 20,000 долл. дают с равными вероятностями либо нулевой валовый доход, либо доход в 100,000 долл. В денежных единицах ожидаемый чистый доход составляет

100,000*0.5 + 0*0.5 - 20,000 = 30,000 долл.

Опираясь на этот вывод, можно было бы заключить, что решение вложить 20,000 долл является оптимальным. Однако подобное решение не в одинаковой степени приемлемо для всех вкладчиков. Например, вкладчик А может полагать, что из-за ограниченности наличных средств потеря 20,000 долл может привести его к банкротству. Следовательно, он, возможно, предпочтет не вкладывать деньги при сложившихся обстоятельствах. Напротив, вкладчик В, располагающий бездействующим капиталом, значительно превышающем необходимую наличность, может охотно пойти на риск.

Этот пример показывает значение отношения лица, принимающего решение, к ценности или полезности денег. Предположим, что А не желает рисковать более чем 5,000 долл. У него есть две возможности:

1) вложить 20,000 долл и получить 100,000 валовой прибыли с вероятностью 1/2;

2) вложить 5,000 долл и получить 23,000 долл с вероятностью 1/2 или с той же вероятностью ничего не получить.

Из этих условий следует, что предпринимателю А ничего не остается, как выбрать вторую альтернативу, хотя ожидаемая в этом случае чистая прибыль в 6,500 долл намного меньше, чем 30,000 долл, ожидаемые при выборе первой альтернативы.

Основной вывод проведенных рассуждений заключается в том, что полезность не обязательно пропорциональна массе денег. Хотя метода построения кривых полезности (зависимостей полезности от массы денег) достаточно разработаны, полезность является столь тонким понятием, что его нелегко определить количественно.

На практике влияние полезности может быть выражено с помощью дополнительных ограничений, отражающих поведение лица, принимающего решение. В нашем примере в качестве такого ограничения выступает максимальный уровень потерь, на которые согласен предприниматель А.

Использование ожидаемых величин предполагает возможность многократного решения одной и той же задачи, пока не будут получены достаточно точные расчетные формулы. Математически это выражается следующим образом.

Пусть z - случайная величина с математическим ожиданием М(z) и дисперсией D(z).

Если (z₁,z₂,...,z_n) - случайная выборка объема n, то выборочное среднее 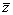= (z₁+z₂+...+z_n)/n имеет дисперсию D(z) / n. Таким образом, когда n ® бесконечность (т.е. становится очень большим), D(z) / n ® 0 и ® М(z).

Другими словами, при достаточно большом объеме выборки разница между выборочном средним и математическим ожиданием стремится к нулю. Следовательно, использование критерия ожидаемого значения допустимо лишь в случае, когда одно и то же решение приходится принимать большое число раз.
Напротив, если необходимость в принятии решения встречается редко, то выборочное среднее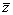
может значительно отличаться от М(z).

Вывод: ориентация на ожидания будет приводить к неверным результатам для решений, которые принимаются небольшое число раз.

Пример. Необходимость в проведении профилактического ремонта оборудования требует принятия решений о том, когда следует проводить плановый ремонт какого-нибудь станка (или другого вида оборудования), чтобы минимизировать потери из-за неисправности (отказа). Если весь временной горизонт разбит на равные периоды, то решение заключается в определении оптимального числа периодов между двумя последующими ремонтами. В случае, когда они производятся слишком часто, затраты на обслуживание будут большими при малых потерях из-за случайных отказов. Компромисс между двумя случаями предусматривает сбалансированный выбор между затратами на ремонт и потерями из-за случайных отказов.

Так как невозможно предсказать заранее, когда возникнет неисправность, необходимо вычислить вероятность того, что станок выйдет из строя в период времени t. В данном случае это и есть элемент риска в процессе принятия решения.

Станок из группы в n станков ремонтируется индивидуально, если он остановился из-за неисправности. Через Т интервалов времени выполняется профилактический ремонт всех n станков. Задача состоит в определении оптимального значения Т, при котором минимизируются общие затраты на ремонт вышедших из строя станков и проведение профилактического ремонта в расчете на один интервал времени.

Пусть p_t - вероятность выхода из строя одного станка в момент t, а n_t - случайная величина, представляющая число вышедших из строя станков в тот же момент. Далее предположим, что c₁ - затраты на ремонт вышедшего из строя станка и c₂ - затраты на профилактический ремонт одного станка.

Применение критерия ожидаемого значения в данном случае оправданно, если станки работают в течение большого периода времени. При этом ожидаемые затраты на один интервал составят:

МC(t)= , где - математическое ожидание числа вышедших из строя станков в момент t. Так как n_t имеет биномиальное распределение с параметрами (n,p_t), то = np_t. Таким образом,

MC(t)=.

Необходимые условия оптимальности для Т* имеют вид

MC(T*-1)>= MC(T*) и MC(T*+1)>= MC(T*).

Следовательно, начиная с малого значения Т, вычисляем МС(Т), пока не будут удовлетворены эти условия.

Положим c₁ = 100 долл, c₂ =10 долл и n =50. Значения p_t приведены в виде таблицы.

	Т	pt		МC(t)
		0,05		$500
		0,07	0,05	$375
T*®		0,10	0,12	$366,7	¬ МС(Т*)
		0,13	0,22	$400
		0,18	0,35	$450

Из этой таблицы видно, что профилактический ремонт необходимо проводить через каждые три (T* =3) интервала времени.

Предположим, что в примере чистая продукция в расчете на один станок в единицу времени составляет а долл и требуется максимизировать доход, приходящийся на единицу времени. Положим также, что доход подсчитывается как разность между общей величиной чистой продукции и затратами на ремонт вышедших из строя станка и обслуживание. Общее выражение для МC(t):

МC(Т)=.

Необходимое условие на Т*, максимизирующего МC(Т):

MC(T*)>= MC(T*-1) и MC(T*)>= MC(T*+1).

Дата добавления: 2014-01-07