
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Факторный эксперимент. Планы первого порядка
|
|
|
|
Планирование полного факторного эксперимента (ПФЭ)
Полным факторным экспериментом называется такой эксперимент, при котором определяется значение выходного параметра или параметра оптимизации Y при всех возможных сочетаниях уровней варьирования факторов.
В эксперимент включают х 1, х 3, …, хk т.е. k – факторов, для каждого из которых следует установить q уровней.
Для осуществления ПФЭ нужно поставить N = qk опытов. Наиболее распространены эксперименты, у которых факторы варьируют на двух уровнях – верхнем и нижнем, т.е. q = 2. Это эксперименты типа 2 k.
Планирование, проведение и обработка результатов ПФЭ включают следующие этапы:
q кодирование факторов;
q составление плана эксперимента или плана-матрицы;
q рандомизацию опытов;
q реализацию плана эксперимента;
q проверку воспроизводимости опытов;
q вычисление и проверку значимости коэффициентов регрессии;
q проверку адекватности регрессионной модели.
Поскольку факторы процесса неоднородны и имеют различные единицы измерения, а числа, выражающие величины факторов, имеют различные порядки, их следует привести к единой системе счисления путем перехода от действительных значений факторов к кодированным по формулам:
 хiосн =
хiосн = 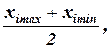 (3.1)
(3.1)
Xi =  (3.2)
(3.2)
Dхi =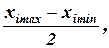 (3.3)
(3.3)
где хiосн – основной уровень фактора;
Xi – кодированное значение фактора;
хimax – верхний уровень фактора;
хimin – нижний уровень фактора;
D хi - интервал варьирования фактора;
i – номер фактора.
Вводят условное обозначение верхнего, нижнего и основного уровней фактора соответственно +1, -1, 0. При построении планов-матриц планирования эксперимента цифры (единицы) можно опускать и писать только их знаки «+» или «-».
Затем строят план-матрицу эксперимента. Построение плана-матрицы сводится к стандартной форме записи условий проведения экспериментов в виде таблицы, в строках которой записывают данные опытов, в столбцах – факторы (в кодах «+» и «-») с реализацией всех возможных сочетаний комбинаций факторов.
В первом столбце таблицы следует менять знаки поочередно, во втором столбце – чередовать их через два, в третьем – через четыре, в четвертом – через восемь и т.д., т.е. по степеням двойки. Общее количество строк в матрице плана для реализации всех возможных сочетаний уровней факторов определяют по формуле N = 2 k.
Например, имеется два фактора Х 1 ,Х 2. Придавая каждому фактору два значения (верхний «+» и нижний «-» уровни), получим четыре возможные сочетания уровней для двух факторов плана матрицы 22 (табл. 3.1). В этом случае больше четырех комбинаций сделать невозможно.
Таблица 3.1
План-матрица ПФЭ 22
| Номер строчки плана | Факторы | |
| Х1 | Х2 | |
| - | - | |
| + | - | |
| - | + | |
| + | + |
Для составления плана-матрицы для трех факторов матрицу планирования (табл. 3.1) повторяют дважды: один раз при значениях Х 3, находящихся на нижнем уровне, второй раз – при значениях Х 3, находящихся на верхнем уровне.
Если же будет рассмотрен четвертый фактор Х 4, то аналогичным образом будет повторено планирование для трех переменных (табл. 3.2): один раз – для фактора Х 4, находящегося на нижнем уровне, второй раз – для фактора Х 4, находящегося на верхнем уровне.
Таблица 3.2
План-матрица ПФЭ 23
| Номер строчки плана | Факторы | ||
| Х1 | Х2 | Х3 | |
| - | - | - | |
| + | - | - | |
| - | + | - | |
| + | + | - | |
| - | - | + | |
| + | - | + | |
| - | + | + | |
| + | + | + |
Аналогично получают планы-матрицы ПФЭ для любого числа факторов.
Пользуясь результатами факторного эксперимента, можно получить описание изучаемой системы или процесса в виде полиномиального уравнения линейной регрессии Y=b 0 +b 1 X 1 +b 2 X 2 +…+bkXk, где выборочные коэффициенты параметров модели процесса b 0, b 1, b 2 и т.д. являются статистическими оценками теоретических коэффициентов 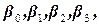 и т.д., а Y – оценка математического ожидания выходного параметра или параметра оптимизации процесса. Можно также получить описание изучаемого процесса в виде полиномиальных уравнений, содержащих эффекты взаимодействия факторов, а также квадратичные члены
и т.д., а Y – оценка математического ожидания выходного параметра или параметра оптимизации процесса. Можно также получить описание изучаемого процесса в виде полиномиальных уравнений, содержащих эффекты взаимодействия факторов, а также квадратичные члены
Y 0 = b 0 X 0 + 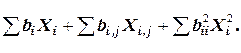
Табл. 3.2 представляет план-матрицу эксперимента, реализовав который, можно подсчитать оценки коэффициентов b 1, b 2, b 3. Однако этих коэффициентов недостаточно, чтобы получить для плана 23 линейное уравнение регрессии вида Y= b 0 + b 1 X 1 + b 2 X 2 + b 3 X 3 либо нелинейное уравнение регрессии, например, вида
Y = b 0 + b 1 X 1 + b 2 X 2 + b 3 X 3 + b 12 X 1 X 2 + b 13 X 1 X 3 + b 23 X 2 X 3 + b 123 X 1 X 2 X 3.
Чтобы получить полный план ПФЭ 2 k для подсчета всех коэффициентов необходимо добавить в план-матрицу еще один столбец – фиктивную переменную Х 0 для оценки свободного члена b 0. Значение Х 0 всегда одинаково во всех строках плана и равно «+1».
Для оценки коэффициентов взаимодействия факторов вводят столбцы со всевозможными комбинациями произведений факторов:
Х 1 Х 2; Х 1 Х 3; Х 2 Х 3; Х 1 Х 2 Х 3.
Поскольку переменные Х 1, Х 2, Х 3 принимают значения «+1» и «-1», то произведения переменных примут те же значения «+1» и «-1». Тогда табл. 3.2 примет следующий вид (табл. 3.3).
Таблица 3.3
Полная план-матрица ПФЭ 23
| № строчки плана | Значения факторов в кодированных обозначениях | Комбинации произведений факторов в кодированных обозначениях | Значение показателя выходной переменной (параметра оптимизации) | ||||||||
| Х0 | Х1 | Х2 | Х3 | Х1 Х2 | Х1 Х3 | Х2 Х3 | Х1 Х2 Х3 | Y1u | Y2u | Yu | |
| + | - | - | - | + | + | + | - | Y 11 | Y 21 | Y 1 | |
| + | + | - | - | - | - | + | + | Y 12 | Y 22 | Y 2 | |
| + | - | + | - | - | + | - | + | Y 13 | Y 23 | Y 3 | |
| + | + | + | - | + | - | - | - | Y 14 | Y 24 | Y 4 | |
| + | - | - | + | + | - | - | + | Y 15 | Y 25 | Y 5 | |
| + | + | - | + | - | + | - | - | Y 16 | Y 26 | Y 6 | |
| + | - | + | + | - | - | + | - | Y 17 | Y 27 | Y 7 | |
| + | + | + | + | + | + | + | + | Y 18 | Y 28 | Y 8 |
Примечание: в рамке, обведенной полужирными линиями, представлен, собственно, план эксперимента ПФЭ 23. Остальные данные необходимы для подсчета коэффициентов уравнения регрессии. Пользуясь такой матрицей планирования, можно приступать к эксперименту. При экспериментировании значениям «+» и «-» соответствуют верхний и нижний уровни факторов в их действительных значениях. Если в каждой строчке плана осуществляется два или более параллельных опыта, то в матрице фиксируется среднее значение из их результатов Y, которое и учитывается при вычислении значений коэффициентов регрессии.
Планы ПФЭ являются симметричными, нормированными, ортогональными и ротатабельными.
Планирование дробного факторного эксперимента (ДФЭ)
Для получения достаточно точных оценок коэффициентов регрессии иногда можно обойтись небольшим количеством опытов, вводя понятия ДФЭ. Если при анализе уравнения регрессии установлено, что какой-либо коэффициент незначим, то переменной или переменными при нем можно пренебречь, но в матрице планирования остается свободный столбец. В него включают новый фактор. Чаще всего незначимыми являются коэффициенты при взаимодействиях, т.е. сами взаимодействия факторов. Их и заменяют новыми факторами.
Дробные факторные эксперименты следует условно обозначать 2 k-p, где р – число факторов, приравненных к незначимым эффектам взаимодействия. При р =1 получают 1/2 ПФЭ, при р =2 получают 1/4 ПФЭ, при р =3 получают 1/8 ПФЭ и т.д. по степени двойки.
Если в ПФЭ (табл. 3.3) один из эффектов взаимодействия (Х 1 Х 2 , Х 1 Х 3 , Х 2 Х 3 или Х 1 Х 2 Х 3) заменить четвертым фактором Х 4 , то получим ДФЭ 24-1, т.е. половину от ПФЭ 24. Если два эффекта взаимодействия заменить факторами Х 4 и Х 5, то получим ДФЭ 25-2, т.е. 1/4 от ПФЭ 25.
Можно получить 1/8 от ПФЭ 26, заменив три эффекта взаимодействия факторами Х 4 Х 5 Х 6 , т.е. ДФЭ 26-3. Если заменить четыре эффекта взаимодействия факторами Х 4 Х 5 Х 6 и Х 7, то получим ДФЭ 27-4, т.е. 1/16 от ПФЭ 27.
Таблица 3.4
План-матрица эксперимента 23-1
| Опыты | Х0 | План | Yu | ||
| Х1 | Х2 | Х3 = Х1Х2 | |||
| + | + | + | + | Y1 | |
| + | - | + | - | Y2 | |
| + | + | - | - | Y3 | |
| + | - | - | + | Y4 |
Можно реализовать другую реплику, где принято Х3 = - Х1Х2. Тогда план-матрица эксперимента примет следующий вид:
Таблица 3.5
План-матрица эксперимента 23-1
| Опыты | Х0 | План | Yu | ||
| Х1 | Х2 | Х3 = - Х1Х2 | |||
| + | + | + | - | Y1 | |
| + | - | + | + | Y2 | |
| + | + | - | + | Y3 | |
| + | - | - | - | Y4 |
Дробный факторный эксперимент следует проводить при числе факторов процесса от двух и более при условиях, когда полный эксперимент по экономическим или другим соображениям проводить не выгодно.
От действительных значений факторов к кодированным переходят так же, как при ПФЭ 2k.
Поскольку при построении планов-матриц ДФЭ произведения комбинаций факторов, между которыми отсутствует эффект взаимодействия, приравнивают к новым факторам, то значения нового фактора в условиях опытов определяют по знакам, указанным в соответствующем столбце незначимого взаимодействия.
Сокращение числа опытов не проходит бесследно: появляется корреляция между некоторыми столбцами матрицы планирования. Это обстоятельство не позволяет раздельно оценивать эффекты факторов и эффекты взаимодействия. Получаются так называемые смешанные оценки (оценки коэффициентов регрессии смешаны с оценками коэффициентов парных взаимодействий):
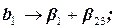

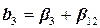 ;
; 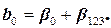

Здесь  ,
, 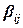 … - коэффициенты регрессии генеральной совокупности данных;
… - коэффициенты регрессии генеральной совокупности данных;
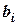 - их выборочные оценки.
- их выборочные оценки.
Матрицы ПФЭ делятся не произвольно, а так, что свойства ортогональности и рототабельности сохраняются при ДФЭ. Для построения дробных реплик используют специальные алгебраические соотношения: генерирующие соотношения (ГС) и определяющие контрасты (ОК).
ГС показывают, какое из взаимодействий принято незначимым, а потому заменено в матрице планирования новой независимой переменной. С ГС можно производить алгебраические операции (умножать обе части равенства). Если фактор встречается в квадрате или другой четной степени, его заменяют на 1. Например, для ДФЭ 23-1 можно записать: Х 3 =Х 1 Х 2 либо Х 3 = -Х 1 Х 2, где Х 1 Х 2 и -Х 1 Х 2 – генерирующие соотношения.
Тогда: Х 1 Х 2 Х 3 =  - Х 1 Х 2 Х 3 =
- Х 1 Х 2 Х 3 = 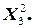
Следовательно: Х 1 Х 2 Х 3 = 1; - Х 1 Х 2 Х 3 = 1.
Это и есть ОК, т.е. соотношения, которые задают элементы первого столбца матрицы, равные 1.
Умножив ОК на каждый фактор, находим соотношения, задающие все смешанные оценки для данной дробной реплики.
Разрешающая способность матрицы максимальная, если линейные эффекты смешаны с наибольшими эффектами взаимодействия по числу входящих в них факторов.
Так, при выборе полуреплики 24-1 возможно 8 решений:
1. Х 4 = Х 1 Х 2 ,
2. Х 4 = - Х 1 Х 2,
3. Х 4 = Х 2 Х 3,
4. Х 4 = - Х 2 Х 3,
5. Х 4 = Х 1 Х 3,
6. Х 4 = - Х 1 Х 3,
7. Х 4 = Х 1 Х 2 Х 3,
8. Х 4 = - Х 1 Х 2 Х 3 .
У последних двух реплик наибольшая разрешающая способность. Они называются главными.
Расчет коэффициентов регрессии и исследование уравнения регрессии при использовании ДФЭ те же, что при ПФЭ. Но можно рассчитывать только те коэффициенты при взаимодействиях факторов, которые определяются столбцами взаимодействий, не совпадающими со столбцами отдельных факторов. Несоблюдение этого правила ведет к нарушению свойств ортогональности плана.
Проверка свойств планов-матриц ПФЭ 2k и ДФЭ 2k-p
После построения плана матрицы ПФЭ 2k и ДФЭ 2k-p необходимо проверить ее свойства.
q Симметричность относительно центра эксперимента: алгебраическая сумма элементов столбца каждого фактора, кроме столбца, отвечающего свободному члену b 0, должна быть равна нулю, т.е.
 , (3.4)
, (3.4)
где u – номер строчки плана-матрицы;
i – номер фактора;
N – общее число строчек плана-матрицы.
q Нормировка: сумма квадратов элементов каждого столбца должна быть равна числу строчек плана-матрицы, т.е.
 2 i u = N. (3.5)
2 i u = N. (3.5)
q Ортогональность: сумма построчных произведений любых двух столбцов плана-матрицы должна быть равна нулю, т.е.
 iu Xju = 0, (3.6)
iu Xju = 0, (3.6)
где Xiu Xju - комбинация факторов в u -й строчке, i ≠ j.
Если план-матрица отвечает вышеперечисленным свойствам, то она соответствует и свойству ротатабельности.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 3132; Нарушение авторских прав?; Мы поможем в написании вашей работы!