Проверка однородности дисперсий и воспроизводимости измерений. Определение ошибки опытов

Рандомизация опытов

Проведение и обработка результатов факторного эксперимента

Перед реализацией плана эксперимента на объекте опыты, предусмотренные в матрице планирования, следует рандомизировать, т.е. установить порядок их проведения в случайной последовательности. Порядок проведения опытов в случайной последовательности следует выбирать по таблице равномерно распределенных случайных чисел или другим способом. Например, требуется провести 8 опытов. Номера строчек в плане матрицы: 1, 2, 3, 4, 5, 6, 7, 8. А установленный случайный порядок реализации опытов может быть, например: 1, 6, 5, 8, 2, 7, 4, 3. Случайный порядок реализации опытов может содержать и кратное восьми число 8 m при выполнении m параллельных измерений в каждой строчке плана. При этом объем выборки m в каждой строчке плана эксперимента по возможности должен быть одинаковым.

По результатам реализации параллельных измерений определяют средние значения показателя отклика (далее - параметра оптимизации) по формуле

Y_u = , (3.7)

где Y_u – среднее арифметическое из m параллельных измерений в строчке с номером u;

Y_uj – действительное значение параметра оптимизации при измерениях в строчке плана с номером u.

Вычисляют построчные дисперсии по данным m параллельных измерений в каждой строчке плана-матрицы по формуле

S 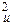= (3.8)

где S 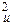- дисперсия в u –той строчке плана-матрицы;

j - порядковый номер параллельного измерения в данной строчке плана-матрицы;

Y_u - среднее арифметическое значение параметра оптимизации из результатов m параллельных измерений Y_uj в u -той строчке.

Находят максимальную дисперсию среди построчных дисперсий, а все построчные дисперсии суммируют.

Для проверки гипотезы однородности дисперсий и воспроизводимости измерений при одинаковом числе m измерений в каждой строчке плана следует пользоваться критерием Кохрена, который вычисляют как отношение максимальной дисперсии к сумме всех построчных дисперсий

G = (3.9)

где G - критерий Кохрена;

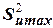- максимальная дисперсия среди построчных;

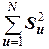- сумма всех построчных дисперсий.

Задав уровень значимости (например, q = 5%), находят табличное значение критерия Кохрена G_табл при числах степеней свободы f₁=m–1 и f₂=N. Если расчетное значение G окажется меньше найденного в таблице, то гипотеза об однородности дисперсий и воспроизводимости результатов измерений принимается. Если проверка дала отрицательный результат, то следует увеличить число параллельных опытов и, по возможности, повысить точность измерений при их выполнении.

Иногда не удается обеспечить равное число параллельных измерений в каждом опыте плана-матрицы.

При разном числе параллельных измерений может быть использован критерий Фишера. Для этого определяют отношение максимальной построчной дисперсии к минимальной

F_расч =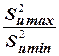. (3.10)

Гипотеза об однородности дисперсий принимается при выполнении условия

F _расч £ F _табл,

где F _табл определено при заданном уровне значимости q и числах степеней свободы fu _max= mu _max-1, fu _min= mu _min-1, где mu _max и mu _min - числа параллельных измерений в строках плана-матрицы, которым соответствуют 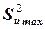и .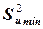

Если построчные дисперсии однородны, т.е. измерения воспроизводимы, то их можно усреднить и найти ошибку опытов 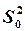и дисперсию воспроизводимости S² _y по формуле

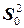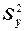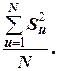= = (3.11)

Число степеней свободы в определении дисперсий 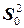= 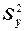: f ₁=N.

В случаях, когда известно, что эксперимент воспроизводим, допускается выполнение m_o параллельных измерений не во всех строчках плана – матрицы, а только в одной из них, чаще всего в центре плана. В таком случае дисперсия опытов может быть рассчитана по формуле

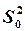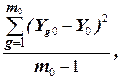= (3.12)

где Y_{g 0} – значение параметра оптимизации с порядковым номером g в центре плана;

Y₀ – среднее арифметическое по результатам m_o опытов в

центре плана;

f₀ = m₀ –1 – число степеней свободы в определении дисперсии.

Примечание: при решении поставленной задачи следует выбирать одинаковый уровень значимости для проверки всех гипотез по критериям Кохрена, Стьюдента, Фишера.

Дата добавления: 2014-01-07