Оценка коэффициентов регрессии, проверка их значимости

Коэффициенты линейной регрессии определяют (одинаково при проведении ПФЭ и ДФЭ) умножением значений Y_u на X_iu в кодовых обозначениях с последующим делением суммы полученных произведений на общее число строчек в плане-матрице, т.е. по формуле

b_i = 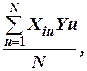(3.13)

где b_i - коэффициенты регрессии 0, 1, 2, …, k;

X_iu - построчные значения фактора в i -том столбце плана-

матрицы;

Y_u - среднее арифметическое по результатам m опытов в

u –той строчке плана-матрицы;

N - общее число опытов или строчек в плане-матрице.

Коэффициенты b_ij рассчитывают по формуле

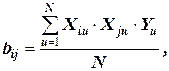i ≠ j. (3.14)

По результатам факторного эксперимента могут быть рассчитаны также коэффициенты b_ii по формуле

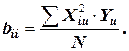(3.15)

Значимость коэффициентов регрессии определяют по t -критерию Стьюдента. В общем случае для каждого коэффициента вычисляют значения t -критерия по формулам:

t_{i =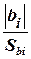} , t_{ij =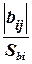} , t_{ii =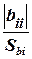} , (3.16)

где | b_i |, | b_ij |, | b_ii | - абсолютные величины рассчитанных коэффициентов регрессии;

S_bi - среднеквадратическое отклонение коэффициентов регрессии.

При числе параллельных опытов m во всех строчках плана-матрицы вычисляют дисперсию определения коэффициента регрессии по формуле

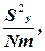= (3.17)

где 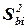– дисперсия коэффициента регрессии b_i;

– дисперсия воспроизводимости параметра оптимизации;

N – общее число строчек в плане-матрице;

m – число параллельных наблюдений в каждой строчке

плана.

Затем определяют среднеквадратическое отклонение (стандартную ошибку) коэффициентов регрессии по формуле

S_bi = 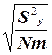. (3.18)

Для проверки гипотезы о значимости каждого коэффициента следует задать уровень значимости q, определить число степеней свободы f₂=N(m-1) и найти в таблице критическое значение коэффициента Стьюдента t_табл. Если расчетное значение критерия t, определенное по формуле (3.16), окажется больше значения t_табл, то гипотеза принимается и коэффициент признается статистически значимым, в противном случае – незначимым.

Для факторного эксперимента может быть рекомендована также другая схема проверки значимости коэффициентов регрессии. Коэффициент считается значимым, если выполняется неравенство

,

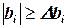где ;

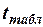- табличное значение критерия Стьюдента при уровне значимости q и f = N степенях свободы дисперсии воспроизводимости.

Если какой-либо коэффициент окажется статистически незначимым, то он может быть отброшен без пересчета остальных коэффициентов.

В полиномиальную математическую модель включают только слагаемые со значимыми коэффициентами.

Статистическая незначимость коэффициентов регрессии b_i может быть обусловлена следующими причинами:

а) основной уровень фактора X_iосн близок к точке частного экстремума;

b) интервал варьирования фактора 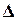X_i выбран малым;

c) данная переменная (или произведение переменных) не имеет статистической связи с параметром Y;

d) велика ошибка эксперимента вследствие наличия неуправляемых и неконтролируемых факторов.

Если имеют место причины, указанные в подпункте а, то значение i -го фактора следует стабилизировать на определенном уровне (не выходя за пределы варьирования). Если имеет место причина, указанная в подпункте b, то следует увеличить интервал варьирования на величину, равную 0,05 ÷ 0,30 от интервала варьирования фактора, т.е. область варьирования должна составлять 10 ÷ 60% от размаха варьирования фактора. Если имеет место причина, указанная в подпункте d, то следует принять меры к уменьшению ошибки эксперимента.

Дата добавления: 2014-01-07