
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Резонанс
|
|
|
|
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой частоте амплитуда колебаний достигает максимального значения.
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой собственной частоте колебательной системы называется резонансом, а соответствующая частота − резонансной частотой.
Найдем резонансную частоту. Амплитуда вынужденных колебаний будет max, когда выражение 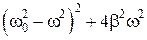 в уравнении
в уравнении 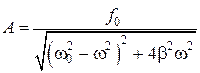 (5.8.13) будет минимальным.
(5.8.13) будет минимальным.
Продифференцируем это выражение по w и приравняем к нулю
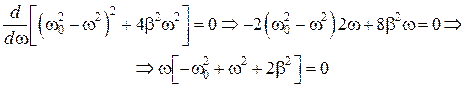 . (5.9.1)
. (5.9.1)
Полученное уравнение имеет три решения: 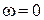 и
и 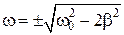 . Первое решение соответствует максимуму знаменателя. Из остальных двух решений отрицательное не имеет физического смысла (частота не может быть отрицательной). Таким образом, резонансная циклическая частота
. Первое решение соответствует максимуму знаменателя. Из остальных двух решений отрицательное не имеет физического смысла (частота не может быть отрицательной). Таким образом, резонансная циклическая частота
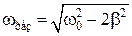 . (5.9.2)
. (5.9.2)
Подставив это значение в выражение для амплитуды (5.8.13), получим выражение для амплитуды при резонансе
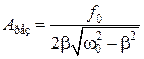 . (5.9.3)
. (5.9.3)
Из последнего уравнения (5.9.3) следует, что при отсутствии
сопротивления среды амплитуда при резонансе обращалась бы в бесконечность, а резонансная частота, согласно (5.9.2), при тех же условиях (при b = 0), совпадала бы с собственной частотой колебаний системы w0.
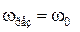 . (5.9.4)
. (5.9.4)
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы показана графически на рис. 5.9.1. В соответствии с (5.9.2) и (5.9.3), чем меньше параметр b, тем выше и правее лежит максимум данной кривой. Изображенная на рис. 5.9.1 совокупность графиков функций (5.8.13), соответствующих различным значениям параметра b, называется резонансными кривыми.
 При стремлении w к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному
При стремлении w к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному 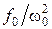 . Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины F 0.
. Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины F 0.
При стремлении w к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия.
Наконец, отметим, что чем меньше b, тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» получается максимум. При малом затухании (т. е.  ) амплитуда при резонансе приближенно равна
) амплитуда при резонансе приближенно равна 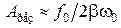 . Разделим это выражение на смещение х 0 из положения равновесия под действием постоянной силы F 0, равное
. Разделим это выражение на смещение х 0 из положения равновесия под действием постоянной силы F 0, равное 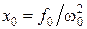 . В результате получим
. В результате получим
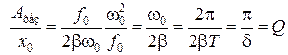 , (5.9.5)
, (5.9.5)
где d = b Т – логарифмический декремент затухания (5.7.2); Q – добротность колебательной системы (5.7.6).
Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы. Следует отметить, что это справедливо лишь при небольшом затухании.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 726; Нарушение авторских прав?; Мы поможем в написании вашей работы!