Теоретическая равномерность подачи

Мгновенная расчетная (геометрическая) подача одного поршня пропорциональна относительной скорости v его движения в цилиндре

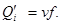
Подставив в данное выражение ранее полученное значение v, получим выражение для мгновенной подачи одного поршня:

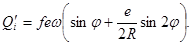
Текущая подача жидкости насосом имеет неравномерный пульсирующий характер. Она слагается из суммы подач отдельных поршней, совершающих в текущий момент рабочий цикл:

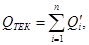
где 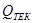и 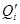- текущие значения расчетной подачи насоса и одного цилиндра;

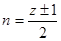- число цилиндров, соединенных в текущий момент с полостью нагнетания.

В полости нагнетания может одновременно находится поршней:

· при нечетном числе цилиндров - ;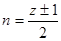

· при четном числе цилиндров - .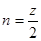

Суммарная мгновенная подача всех поршней, находящихся в рабочей полости, составит

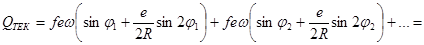
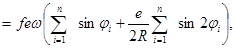
где 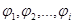- текущие углы поворота, образованные осями цилиндров – осью мертвых положений.

Из выражения суммарной мгновенной подачи всех поршней (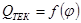) следует, что поскольку одновременно действует несколько поршней (замыкателей), каждый из которых принимает участие в процессе нагнетания в течение конечного, весьма короткого промежутка времени, и подача носит дискретный характер, расчетная подача жидкости насосом будет пульсирующей, причем чем больше число поршней, тем меньше будет амплитуда и больше частота пульсаций подачи. Для однорядных насосов с четным числом цилиндров число пик, приходящееся на угол поворота 180⁰, равно числу цилиндров, а для насосов с нечетным числом – удвоенному числу цилиндров. Амплитуда пульсаций подачи при нечетном числе цилиндров будет соответственно меньшей, чем при четном.

Т.к. по окружности блока цилиндров расположено z поршней, то образуется z сдвинутых по фазе 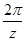кривых подачи отдельных поршней. В результате колебание суммарного расхода поршней составляет относительно небольшую величину.

На рис. 4 приведены расчетные графики колебания подачи жидкости с числом цилиндров z = 5 и z = 6 в функции угла 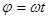поворота цилиндрового блока, расчитанные по формуле 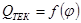. Заштрихованные участки характеризуют степень неравномерности подачи. Более высокая неравномерность подачи при четном числе цилиндров обусловлена тем, что цилиндры расположены диаметрально противоположно, т.е. в мертвом положении здесь одновременно

φ

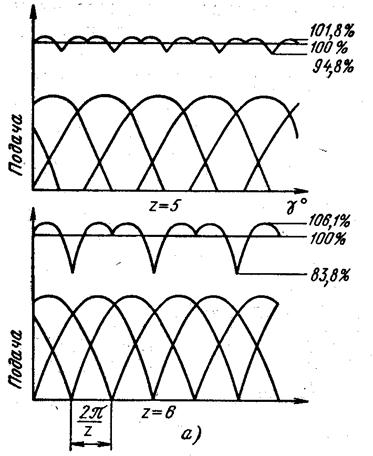будут находится два цилиндра.

φ

Рис. 4. График колебания подачи в радиально-поршневом насосе

Поскольку величина R значительно превышает величину эксцентриситета е, вторым членом уравнения 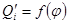можно пренебречь; в результате получим чисто синусоидальный закон мгновенной подачи одним поршнем

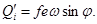
Дата добавления: 2014-01-07