
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вторая теорема Фробениуса
|
|
|
|
Определение 7
Определение 6
Вектор-функция 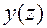 , удовлетворяющая определению 5,называется решением задачи Коши системы уравнений (2.3.35), проходящим через точку
, удовлетворяющая определению 5,называется решением задачи Коши системы уравнений (2.3.35), проходящим через точку 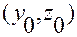 .
.
Система (2.3.35) называется вполне интегрируемой в области 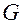 , если она интегрируема при любых
, если она интегрируема при любых 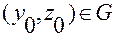 .
.
Необходимые и достаточные условия интегрируемости системы (2.3.35) даются второй теоремойФробениуса.
Теорема 4 (вторая теорема Фробениуса)
Для того чтобы система (2.3.35)
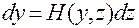 (2.3.35)
(2.3.35)
была вполне интегрируема в области 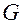 , необходимо и достаточно, чтобы выполнялись следующие условия:
, необходимо и достаточно, чтобы выполнялись следующие условия:
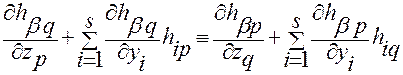 (2.3.36)
(2.3.36)
для всех  ;
;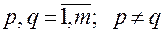 .
.
Тождества (2.3.36) рассматриваются по всем значениям переменных 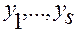 ,
, 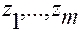 в области
в области 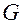 .
.
Вывод формулы (2.3.36) дается в Дополнении 5 при доказательстве необходимости условий теоремы 4 (см. стр. 48).
4.4. Пример интегрируемой системы, состоящей
из двух неинтегрируемых связей
Обратимся к примеру из предыдущего пункта (п.3º).
Приведем систему (2.3.32)
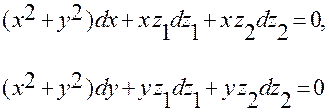 (2.3.32)
(2.3.32)
к виду (2.3.35):
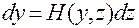 . (2.3.35)
. (2.3.35)
Обозначим
 ,
,  ,
,  .
.
Тогда, разделив первое и второе уравнения на  , придем к системе:
, придем к системе:
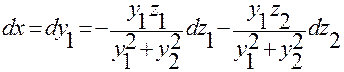 ,
,
 .
.
Правые части определены при всех  , кроме множества
, кроме множества
 .
.
Имеем
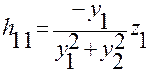 ,
, 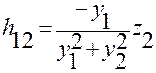 ,
,
 ,
,  .
.
Проверим выполнение условий второй теоремы Фробениуса:
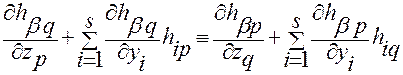 (2.3.36)
(2.3.36)
для всех  ;
; .
.
Полагаем для связи с номером  значения индексов
значения индексов 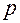 и
и 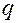 :
:
а)  ; б)
; б)  .
.
Следует заметить, что условия Фробениуса симметричны относительно  при любом фиксированном
при любом фиксированном 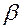 .
.
Поэтому проверять их можно только для значений  (или
(или  ).
).
В нашем случае достаточно рассмотреть только  (при
(при  ).
).
Запишем левую часть условия (2.3.36):
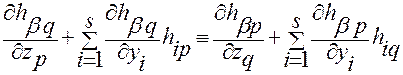 (2.3.36)
(2.3.36)
при  ,
,  с учетом того, что:
с учетом того, что:
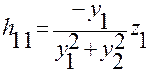 ,
, 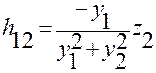 ,
,
 ,
,  .
.
Получим


 .
.
Легко видеть, что она приводится к виду:
 . (2.3.42)
. (2.3.42)
Вычислим правую часть условий Фробениуса (2.3.36):
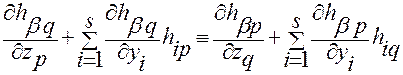 (2.3.36)
(2.3.36)
для  ,
,  с учетом того, что:
с учетом того, что:
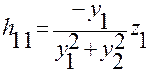 ,
, 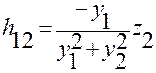 ,
,
 ,
,  .
.
Получим



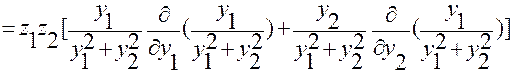 . (2.3.43)
. (2.3.43)
Сопоставляя (2.3.42) и (2.3.43):
 , (2.3.42)
, (2.3.42)
видим, что условия Фробениуса для  выполняются.
выполняются.
Проверим эти условия для  и
и  .
.
Вычислим левую часть (2.3.36):
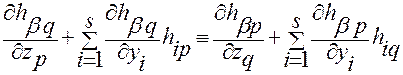 (2.3.36)
(2.3.36)
с учетом того, что:
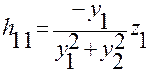 ,
, 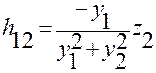 ,
,
 ,
,  .
.
Получим:
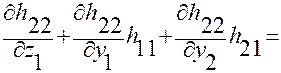

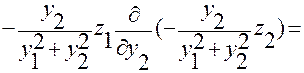
 .
.
Аналогично находим выражение для правой части
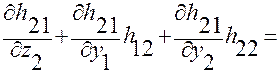


 .
.
Сопоставляя левую:

и правую части, видим, что они совпадают, т.е. условия Фробениуса для  выполняются.
выполняются.
Таким образом, выполнены все условия второй теоремы Фробениуса. Поэтому система (2.3.32):
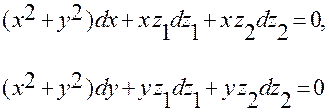 (2.3.32)
(2.3.32)
вполне интегрируема при  .
.
Пример показывает, что если уравнение хотя бы одной дифференциальной связи не интегрируемо, то это еще не значит, что в совокупности с другими уравнениями связей оно не будет интегрируемо.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 765; Нарушение авторских прав?; Мы поможем в написании вашей работы!