Понятие множества возможных положений

Определение 16

Определение 15

Механическая система называется голономной, если все связи, накладываемые на нее кинематическим способом, являются голономными.

Такая система называется стационарной голономной, если все эти связи стационарны.

Если хотя бы одна из связей нестационарная, то голономная механическая система называется нестационарной.

Механическая система называется неголономной, если среди связей, накладываемых на нее кинематическим способом, имеется хотя бы одна кинематическая, т.е. имеется хотя бы одна связь, неинтегрируемая в любой совокупности с другими дифференциальными связями.

Такая система называется стационарной неголономной системой, если все ее связи (и голономные, и неголономные) являются стационарными.

В противном случае она называется нестационарной неголономной системой.

§4. Обобщенные координаты голономной системы.
Число степеней свободы

1º. Требования, накладываемые на уравнения
голономных связей

Будем рассматривать механические системы с голономными связями.

Сформулируем требования, которым должны удовлетворять уравнения голономных связей.

Математические модели голономных связей в общем случае образуют систему равенств вида

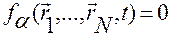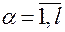, . (2.4.1)

Сюда включены и интегрируемые дифференциальные связи, предварительно проинтегрированные.

Аргументами функций 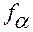являются время 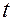и векторы

, ,

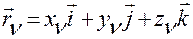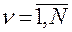где — координаты точки 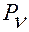, , 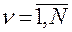механической системы в выбранной системе отсчета.

Будем смотреть на эти равенства как на систему уравнений относительно положений 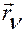, , 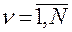точек механической системы, считая при этом время 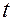параметром.

Ясно, что при таком взгляде на систему уравнений (2.4.1) можно трактовать эту систему следующим образом.

Она определяет (задает) в каждый момент времени 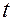множество допустимых положений материальных точек — положений, которые «связи позволяют материальной системе занимать в момент времени ».

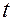Такие положения будем называть возможными или допустимыми положениями механической системы, а совокупность положений 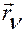, , 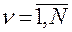являющихся решением системы уравнений (2.4.1) в фиксированный момент времени 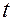, — множеством допустимых (возможных) положений в этот момент времени.

Дата добавления: 2014-01-07