Предмет кинематики. Системы отсчета

Лекция № 1

Элементы кинематики

1.1. Предмет кинематики. Системы отсчета.

1.2. Способы задания движения материальной точки.

1.3. Средние, мгновенные скорости и ускорения.

Кинематика (от греч. движение) − раздел механики, посвященный изучению движения материальных объектов без учета их масс и действующих на них сил, т. е. кинематика рассматривает движение без учета причин, его вызывающих. Устанавливаемые здесь закономерности используются при кинематических исследованиях движений, в частности, при расчете механических передач в различных технических устройствах, а также при решении задач динамики.

Основной задачей кинематики является расчет кинематических характеристик движущихся объектов, к которым относятся скорость, ускорение и траектория.

В зависимости от изучаемого объекта выделяют кинематику материальной точки, твердого тела и непрерывно распределенной среды (деформируемого твердого тела, жидкости, газа).

Для описания движения необходимо выбрать систему отсчета.

Система отсчета состоит из тела отсчета и системы пространственных координат, снабженной часами и связанной с телом отсчета.

Тело отсчета − произвольно выбранное, в идеале − абсолютно твердое тело, относительно которого определяется положение остальных тел.

1.2. Способы задания движения материальной точки

При векторном способе задания движения положение материальной точки в данный момент времени характеризуется радиус-вектором 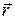, проведенным из начала координат в данную точку (рис. 1.2.1).

При движении материальной точки конец радиус-вектора описывает в пространстве кривую, которая называется траекторией движущейся точки. В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Длина и направле ние радиус-вектора изменяется со временем согласно некоторому закону 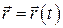, который называется уравнением движения материальной точки.

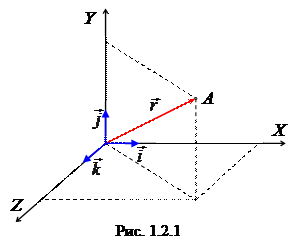При координатном способе задания движения используется декартова система координат. Положение материальной точки в данный момент времени характеризуется тремя координатами X, Y и Z, а перемещение может быть представлено как результат трех независимых перемещений вдоль координатных осей: x = x (t), y = y (t), z = z (t).

. (1.2.1)

1.3. Средние, мгновенные скорости и ускорения

Для характеристики движения вводится понятие вектора скорости, который определяет как быстроту движения, так и направление в данный момент времени.

Средней скоростью на некотором участке MN называется величина равная отношению перемещения 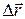к промежутку времени D t, за который это перемещение произошло

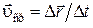. (1.3.1)

Вектор мгновенной скорости есть предел, к которому стремится вектор при стремлении D t ® 0, т. е.

. (1.3.2)

При 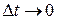направление вектора 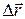стремится к касательной к траектории в точке 1. Кроме того, что при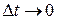 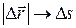, поэтому модуль скорости 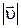равен

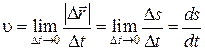. (1.3.3)

В декартовых координатах

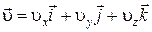, (1.3.4)

где

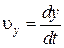, , (1.3.5)

есть проекции скорости 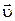на оси х, у, z. Модуль скорости

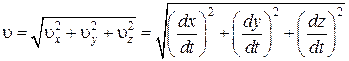. (1.3.6)

Быстрота изменения скорости со временем характеризуется ускорением. Ускорение равно первой производной от вектора скорости 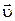или второй производной от радиус-вектора 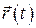по времени. Ускорение − это векторная величина

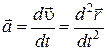. (1.3.7)

Ускорение можно найти по его проекциям на оси координат

, (1.3.8)

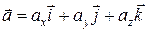. (1.3.9)

Модуль

. (1.3.10)

Дата добавления: 2014-01-07