Лекция № 2. 1.4. Нормальное и тангенциальное ускорения при криволинейном движении

Элементы кинематики

1.4. Нормальное и тангенциальное ускорения при криволинейном движении.

1.5. Классификация движений материальной точки.

1.6. Кинематика абсолютно твердого тела.

1.7. Связь между линейными и угловыми характеристиками тела при его вращении.

1.4. Нормальное и тангенциальное ускорения при криволинейном движении

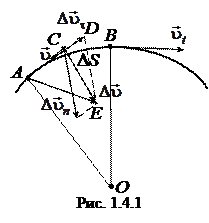В общем случае при движении тела его скорость изменяется как по величине, так и по направлению. Для характеристики быстроты изменения скорости движения вводится понятие ускорения.

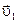Рассмотрим плоское движение, т. е. такое, при котором все участки траектории точки лежат в одной плоскости. Пусть вектор задает скорость точки А в момент времени t. За время D t движущаяся точка перешла в положение В и приобрела скорость, отличную от u как по модулю, так и направлению и равную . Перенесем вектор в точку А и найдем 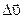(рис.). Средним ускорением 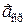неравномерного движения в интервале времени от t до t +D t называется векторная величина, равная отношению изменения скорости 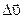к интервалу времени D t:

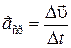. (1.4.1)

Ускорение в данный момент времени (мгновенное ускорение) представляет собой предел, к которому стремится выражение (1.4.1) при 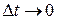, т. е.

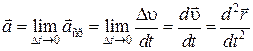. (1.4.2)

Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.

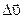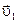Разложим вектор на две составляющие. Для этого из точки А (рис. 1.4.1) по направлению скорости отложим вектор , по модулю равный . Очевидно, что вектор 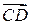, равный 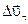, определяет изменение скорости по модулю за время D t: 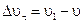. Вторая же составляющая 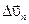вектора 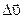характеризует изменение скорости за время D t no направлению.

Тангенциальная составляющая ускорения

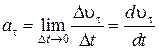, (1.4.3)

т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

Определим вторую составляющую ускорения. Допустим, что точка В близка к точке А, поэтому D s можно считать дугой окружности некоторого радиуса r, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и ЕАD следует Du_n/ АВ =u₁/ r, но так как АВ =uD t, то Du_n/D t =uu₁/ r. В пределе при D t ®0, получим ®.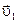

Поскольку 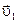®, угол ЕАD стремится к нулю, а так как треугольник ЕАD равнобедренный, то угол АDE между и 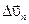стремится к прямому. Следовательно, при D t ®0 векторы и 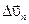оказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор 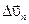, перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная

. (1.4.4)

называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны. Поэтому эту составляющую ускорения называют также центростремительным ускорением.

Таким образом, полное ускорение тела 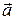есть геометрическая сумма тангенциальной 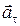и нормальной 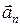составляющих

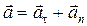, (1.4.5)

Тангенциальное ускорение равно первой производной по времени от модуля скорости и определяет быстроту изменения скорости по модулю, и направлено по касательной к траектории.

Нормальное ускорение определяет быстроту изменения скорости по направлению и направлено к центру кривизны траектории.

Векторы 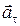и 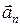взаимно перпендикулярны поэтому модуль полного ускорения равен

. (1.4.6)

1.5. Классификация движений материальной точки

В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:

1) a _t = 0, a_n = 0 − прямолинейное равномерное движение.

2) a _t = const, a_n = 0 − прямолинейное равнопеременное движение.

При таком движении 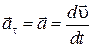. Проинтегрировав это выражение, получим:

Þ Þ .

Так как 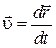, то, проинтегрировав полученное выражение в пределах от нуля до произвольного момента времени можно найти перемещение точки:

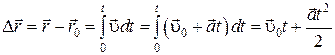
или .

3) a _t = f (t), a_n = 0 − прямолинейное движение с переменным ускорением.

4) a _t = 0, a_n = const. При таком движении скорость точки не изменяется по модулю, так как тангенциальная составляющая равна нулю, а изменяется только по направлению.

5) a _t = const, a_n ¹ const − равнопеременное движение по окружности.

6) a _t = 0, a_n ¹ 0 − равномерное криволинейное движение.

7) a _t = const, a_n ¹ 0 − криволинейное равнопеременное движение.

1.6. Кинематика абсолютно твердого тела

Вращательное движение − это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. При вращательном движении скорости и ускорения различных точек тела неодинаковы. Поэтому в качестве общих кинематических характеристик движения тела при вращении вводятся угол поворота, угловая скорость и угловое ускорение тела. При вращении тела угол поворота изменяется со временем по некоторому закону j = j(t), который называется уравнением вращательного движения тела.

Угловой скоростью тела называется вектор, численно равный первой производной по времени от угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:

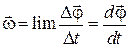. (1.6.1)

Вектор угловой скорости направлен по оси вращения, причем так, чтобы вращение, рассматриваемое с конца вектора угловой скорости, происходило против хода часовой стрелки (рис 1.6.1). Единицей угловой скорости является рад/с.

Скорость произвольной точки вращающегося тела назы-
вается линейной скоростью этой точки.

При равномерном враще-
нии угловая скорость не изменя-
ется со временем, то есть явля-
ется постоянной величиной (w =
= const). Тогда

.

Равномерное вращение характеризуется периодом вращения и частотой вращения.

Период вращения − это время, за которое точка совершает один полный оборот, т. е. поворачивается на угол j = 2p и на основании выражения (1.6.1) .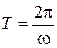

Частота вращения − это число полных оборотов, которое делает точка при равномерном вращении, за единицу времени: 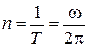, откуда w = 2p n.

Для характеристики неравномерного вращения тела вводится понятие углового ускорения.

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

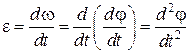. (1.6.2)

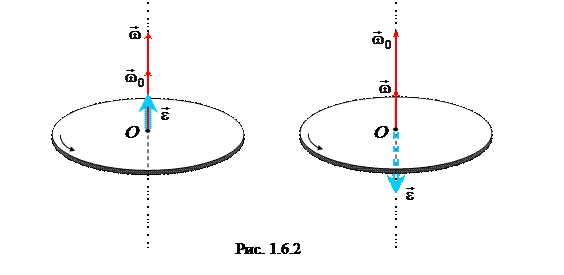
При ускоренном вращении вектор углового ускорения сонаправлен с вектором угловой скорости, а при замедленном − противоположен ему.

В случае равнопеременного движения точки по окружности (e =
= const) угловая скорость определяется по формуле

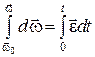Þ 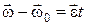Þ Þ 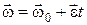. (1.6.3)

Или в скалярном виде

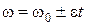. (1.6.4)

Проинтегрировав выражение (1.6.1) можно получить формулу для угла поворота тела

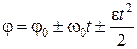. (1.6.5)

Исключив из последнего уравнения 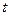, получим

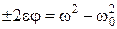, (1.6.6).

где j = 2p N, N − число полное число оборотов, совершенных телом.

В случае e = e(t), угловая скорость и закон вращательного движения определяются следующими формулами

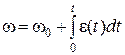, . (1.6.7)

Рис. 4

1.7. Связь между линейными и угловыми характеристиками тела при его вращении

За время dt точка проходит по дуге окружности радиуса R путь dS = Rd j. Поэтому 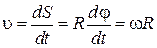. Если угол поворота враща-ющегося тела представить в виде d j = w(t) dt и проинтегрировать в пределах от начального момента времени t ₁ до конечного момента времени t ₂, то получится угол, на который совершила поворот тело за время: .

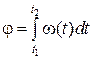Тангенциальная и нормальная составляющие ускорения произвольной точки тела, вращающегося вокруг неподвижной оси, определяются формулами:

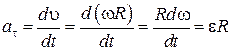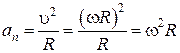, . (1.7.1)

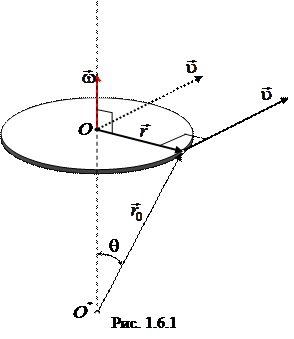
Полученные соотношения (1.7.1) можно записать в векторном виде. Для этого на оси вращения ОО ^* (рис. 1.6.1) тела выберем любую точку A и проведем из нее радиус-вектор 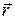в точку M. Векторное произведение 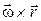по модулю и направлению совпадает с вектором скорости 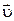точки M:

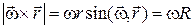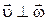, и 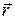. (1.7.2)

Следовательно, можно записать, что вектор скорости 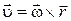, а вектор ускорения точки

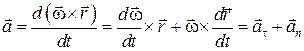. (1.7.3)

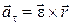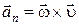, . (1.7.4)

Дата добавления: 2014-01-07