Основные понятия исчисления предикатов

Исчисление высказываний позволяет строить только весьма примитивные логические рассуждения. Большинство же математических и обычных рассуждений нельзя провести средствами исчисления высказываний.

Хрестоматийный пример. Очевидное рассуждение: «Все люди смертны. Сократ – человек, следовательно, Сократ смертен» нельзя обосновать средствами исчисления высказываний. Дело в том, что высказывание в исчислении высказываний – это простое повествовательное предложение, которое рассматривается как неделимое целое. Его нельзя разобрать на составные части, чтобы проанализировать связь между ними. Но именно такой анализ требуется для доказательства смертности Сократа. Проведем его. Утверждение «Все люди смертны» по-другому можно сформулировать так. Для всякого x верно, что если x - человек, то x - смертен. Значит, если заменить букву x именем любого человека, то окажется справедливым заключение о смертности этого человека. В частности, смертен Сократ.

Исчисление высказываний можно расширить, введя три новых понятия – термы, предикаты, кванторы, после чего возможности анализа рассуждений значительно расширятся.

Определение. Предметной переменной назовем строчную букву, быть может, с верхним или нижним индексом, из конца латинского алфавита.

Определение. Предметной константой (постоянной) назовем строчную букву, быть может, с верхним или нижним индексом, из начала латинского алфавита. Далее для обозначения констант мы будем использовать и буквы греческого алфавита.

Определение. Запись вида 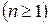назовем n- местным функциональным символом. Эти символы используются для обозначения функций n переменных.

Определение. Предметные переменные и предметные константы называются термами. Кроме того, если 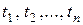- термы и f – n -местный функциональный символ, то запись - тоже терм.

Определение. Запись вида 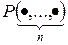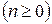назовем n- местным предикатным символом.

Определение. Если 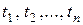- термы и P – n -местный предикатный символ, то запись 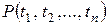назовем n- местным предикатом.

Произвольный набор предикатных и функциональных символов, для каждого из которых указано соответствующее значение 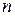, называется сигнатурой.

А теперь предадим содержательный смысл введенным определениям.

Условимся, что все предметные переменные и предметные константы принимают значения из некоторого множества D, которое называется универсумом или предметной областью, или полем.

Условимся, что всякому терму поставлена в соответствие некоторая функция . Известно, какое значение из поля D принимает функция f на каждом допустимом наборе значений своих аргументов.

Наконец, положим, что всякому n -местному предикату 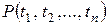приписана некоторая логическая функция, принимающая значение И (истина) или Л (ложь) на каждом наборе значений своих аргументов. Нульместному предикату P приписывается некоторое высказывание, которое может быть либо истинным, либо ложным.

В этом случае говорят, что определена интерпретация данной сигнатуры.

В более узком смысле под n -местным предикатом понимается функция n переменных , область значений которой – это предложения. В этих предложениях переменные (термы) являются подлежащими или дополнениями, а также некоторыми обстоятельствами, выраженными существительными. После подстановки в такие предложения вместо символов некоторых конкретных значений предложение становится высказыванием, истинным или ложным.

Пример 1. «Джон любит x» - одноместный предикат. Если вместо буквы x подставлять имена объектов, получаются высказывания. Они могут быть истинными, ложными или бессмысленными, если заранее разумно не определить область значений переменной x. Так, высказывание «Джон любит Мери», «Джон любит футбол», «Джон любит ванильное мороженное» имеют смысл. А высказывание «Джон любит черную дыру» вряд ли можно считать осмысленным.

Пример 2. «x любит y» - это двухместный предикат. И в этом случае следует позаботиться о разумном выборе области определения переменных x и y. Такое, например, высказывание, как «ванильное мороженное любит футбол», безусловно, не имеет смысла.

Пример 3. «x + y = z» - это трехместный предикат. В качестве универсума D можно, например, выбрать множество R вещественных чисел. Тогда высказывание «2 + 7 = 9» - истина, высказывание «2,1 + 7,3 = 9» - ложь.

Обратимся к понятию квантора.

Утверждение «всякое рациональное число есть действительное число» можно высказать по-другому: «для всякого x верно, что если x – рациональное число, то x – действительное число». Выражение «для всякого x» назовем квантором всеобщности. Будем считать выражения «для всякого x», «для любого x», «для каждого x», «для всех x» тождественными друг другу и писать: .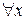

Обозначим через Q (x) предикат «x – рациональное число», через R (x) предикат «x – вещественное число». Тогда формула есть формальная запись высказанного утверждения о включении множества рациональных чисел во множество действительных чисел.

Утверждение «некоторые действительные числа являются рациональными числами» можно сформулировать так: «существуют такие x, что x – действительное число и x – рациональное число».

Выражение «существуют такие x» назовем квантором существования. Будем считать, что записи «существуют такие x», «для некоторых x», «по крайней мере для одного x» имеют одинаковый смысл и обозначим любую из них как .

Тогда утверждение о непустом пересечении множеств вещественных и рациональных чисел выражается формулой &.

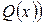Дата добавления: 2014-01-07