Формулы исчисления предикатов

Опишем, как строятся формулы исчисления предикатов.

Всякая формула состоит из атомарных формул, соединенных логическими связками.

Определение. Если 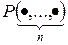- n -местный предикатный символ и 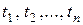- термы, то 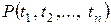- атомарная формула.

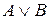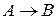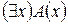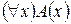Определение. Если А – формула, то (А), - формулы. Если А и В – формулы, то ; А & В; - формулы. Если А (х) – формула, содержащая переменную х, то и - формулы. Других формул нет.

Замечание 1. Вместо знака отрицания часто удобнее пользоваться знаком .

Замечание 2. Если в формулу входят символы отрицания и кванторы, то порядок их расположения имеет значение не только с формальной точки зрения, но и с точки зрения смысла формулы.

Пусть, например, P (x) = «x – блестящий знаток математической логики». Тогда запись означает «не всякий x является блестящим знатоком математической логики», а смысл формулы 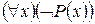таков: «всякий x не является блестящим знатоком математической логики».

Замечание 3. Если перед предикатом от нескольких переменных поставить квантор для одной из них, переменная под знаком квантора перестает быть аргументом предиката.

Пример 1. Пусть Р (х, у) = «х делит у», 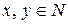. Тогда «7 делит 5» - ложное высказывание; «2 делит 6» - истинное. Формула 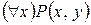уже задает одноместный предикат: «Всякое натуральное число делит у». Какое бы значение у из области определения не подставлять в эту формулу, всегда получится ложь. Формула 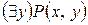представляет собой функцию переменной х: «существует число, которое делится на х». Это истина для всякого натурального х.

А формулы 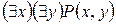, , , 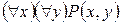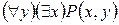уже вообще не зависят от аргументов х и у. Эти формулы представляют собой высказывания: «существуют такие натуральные числа, что одно из них делит другое» - истина; «существует натуральное число, которое делит всякое натуральное число» - истина (1 делит все натуральные числа); «всякое натуральное число делит все натуральные числа» - ложь; «у всякого натурального числа есть делители» - истина (простое число делится на 1 и само на себя).

Если предложение Р (х, у) сформулировать в виде «х делит у и 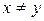, 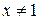» то высказывание 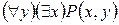становится ложным.

Пример 2. Высказывание 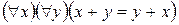- это истинное высказывание, утверждающее коммутативность сложения. Высказывание 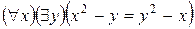- истинно, достаточно положить у = х. Высказывание 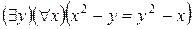- ложно. Одного и того же значения у для всех значений х не существует.

Дата добавления: 2014-01-07