Примеры решения задач. Пример 1. Пусть Р(х) = «х – простое число», Е(х) = «х – четное число», Q(x) = «x – нечетное число», D(x

Пример 1. Пусть Р (х) = «х – простое число», Е (х) = «х – четное число», Q (x) = «x – нечетное число», D (x, y) = «x делит y». Универсум D – множество целых чисел.

Перевести на русский язык:

P (7), E (2)& P (2), ,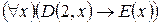

.

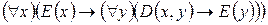Решение: P (7) = «7 – простое число», E (2)& P (2) = «2 – четное и простое число», 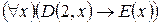= «всякое число, которое делится на 2 - четное», 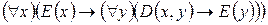= «всякое число, делящееся на четное число, само четно».

Пример 2. Ниже помещены четыре предложения на русском языке, за которыми следуют столько же формул исчисления предикатов. Соединить в пары эти предложения, чтобы члены пары были эквивалентны. В скобках указаны обозначения соответствующих предикатов.

1. Все судьи – юристы (J (x), L (x), от английского judge – судья, lawyer - юрист).

2. Некоторые юристы – жулики (S (x), от английского swindler - мошенник).

3. Ни один судья не является жуликом.

4. Некоторые юристы восхищаются только судьями (A (x, y), от английского admire - восхищаться).

1!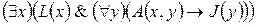

2!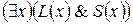

3!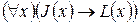

4!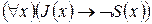

Решение: 1 – 3!; 2 – 2!; 3 – 4!; 4 – 1!

Справедливость заключений вида «для всех» и «для некоторых», основанных на такого же вида посылках, можно неформально проверять, считая посылки верными, при помощи диаграмм Венна. Всякое утверждение вида «для всех» означает включение одного множества в другое. Утверждение вида «для некоторых» означает непустое пересечение множеств.

Соответствующие множества изображаются областями внутри универсума. Если можно построить такую диаграмму, на которой в условиях истинности посылок заключение не выполняется (нет вложений одного множества в другое, пересечение множеств пусто), то вывод не верен. В противном случае из данных посылок построен правильный вывод.

Пример 3. Проверить правильность (ложность) умозаключения при помощи диаграмм Венна.

Некоторые адвокаты богаты. Некоторые врачи богаты. Значит некоторые врачи – адвокаты.

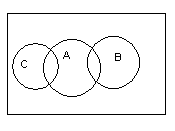
Решение: Универсум – множество всех людей. Пусть А – множество богатых людей, В – множество адвокатов, С – множество врачей. В посылках говорится о непустом пересечения множеств А и В; А и С. В заключении утверждается, что Ø, так ли это? На построенной диаграмме показана возможность пустого пересечения множеств В и С, заключение неверно.

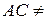Ø; 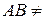Ø; ВС = Ø 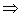заключение ложно

Переведем посылки и заключения на язык исчисления предикатов. Пусть А (х) = «х - богат», В (х) = «х - адвокат», С (х) = «х - врач». Дано: 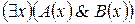; 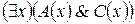. Верно ли, что ?

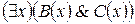Пример 4. проверить правильность умозаключения при помощи диаграмм Венна.

Все поэты счастливы. Некоторые поэты ленивы. Значит, некоторые ленивые люди счастливы.

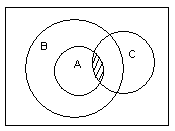
Решение: Пусть А – множество поэтов, В – множество счастливых людей, С – множество ленивых людей, универсум – множество всех людей.

Дано: 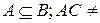Ø. Верно ли, что Ø?

На диаграмме Венна видно, что непустое пересечение АС принадлежит множеству В (это легко доказать строго), поэтому ВС заведомо не пусто.

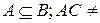Ø 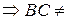Ø, заключение верно.

На языке исчисления предикатов: если верно, что 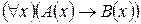и 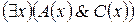, то верно также, что .

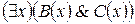Дата добавления: 2014-01-07