
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Анализ геометрической стороны задачи. Выражение перемещений и деформаций через прогибы
|
|
|
|
В силу гипотезы плоского напряженного и деформируемого состояния
 , но по формуле Коши
, но по формуле Коши  , следовательно, функция прогибов не зависит от координаты z, т.е. прогибы на всем прямолинейном нормальном к поверхности плиты элементе одинаковы. Иными словами, функция прогибов
, следовательно, функция прогибов не зависит от координаты z, т.е. прогибы на всем прямолинейном нормальном к поверхности плиты элементе одинаковы. Иными словами, функция прогибов
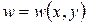 . На рисунке 27 прогиб точки «k» есть отрезок «
. На рисунке 27 прогиб точки «k» есть отрезок « ». Прогибы всех точек, лежащих на нормали «ML» одинаковы.
». Прогибы всех точек, лежащих на нормали «ML» одинаковы.
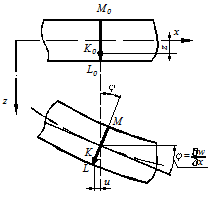
Рисунок 27
В силу гипотезы прямых нормалей нет сдвигов между нормалью и срединной изогнутой поверхностью, т.е.
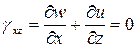
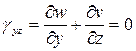
Разделяя переменные в выше приведенных соотношениях и интегрируя по z в пределах толщины плиты, получим выражения перемещений через прогибы
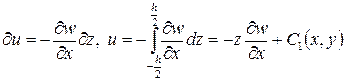
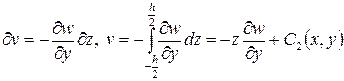
Для определения функций, полученных при интегрировании 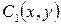 и
и 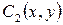 воспользуемся гипотезой нейтрального срединного слоя: при
воспользуемся гипотезой нейтрального срединного слоя: при  , тогда
, тогда 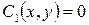 и
и  . Таким образом, окончательно выразили перемещения через прогибы в плитах
. Таким образом, окончательно выразили перемещения через прогибы в плитах
 ,
,  (9)
(9)
Эти соотношения легко иллюстрируются (Рис. 27). Перемещение точки «N» по оси x равно произведению расстояния от точки до нейтрального слоя на тангенс угла наклона нормали к вертикали (тангенс угла наклона касательной к оси x).
Используя формулы Коши и зависимости (9), получим выражение деформаций через прогибы
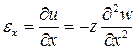
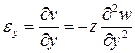
 (10)
(10)
Имея эти соотношения, можем выразить напряжения через прогибы плиты.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 602; Нарушение авторских прав?; Мы поможем в написании вашей работы!