КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основное уравнение изгиба плит
|
|
|
|
Выражение поперечных сил через прогибы плиты
Используя первые два дифференциальных уравнения равновесия плит (8), из первого получим
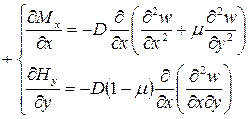
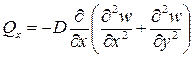(22)
Аналогично из второго дифференциального уравнения равновесия (8) получаем выражение для поперечной силы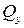 
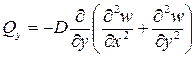(23)
Подстановка поперечных сил в третье дифференциальное уравнение равновесия (8) связывает прогибы с внешней нагрузкой
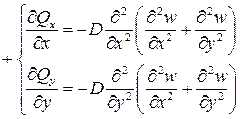
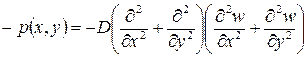
После изменения знаков и деления на цилиндрическую жесткость окончательно получаем основное уравнение изгиба плит
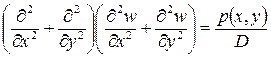(24)
Это уравнение носит название уравнения Софи Жермен и Лагранжа. Оно может быть записано в развернутом виде
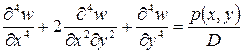(24-а)
или в сокращенных видах
, 
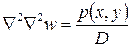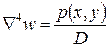(24-б,в)
В выражениях (24-б.в) введен оператор Лапласа
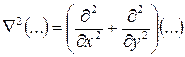
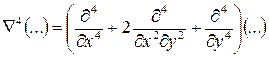(25)
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 406; Нарушение авторских прав?; Мы поможем в написании вашей работы!