Уравнение плоской волны

Уравнением плоской волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x, y, z и времени t

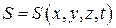. (6.2.1)

Эта функция должна быть периодической как относительно времени t, так и относительно координат x, y, z. Периодичность по времени вытекает из того, что смещение 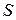описывает колебания частицы с координатами x, y, z, а периодичность по координатам следует из того, что точки, отстоящие друг от друга на расстоянии, равном длине волны, колеблются одинаковым образом.

Предположим, что колебания носят гармонический характер, а ось 0 х совпадает с направлением распространения волны. Тогда волновые поверхности будут перпендикулярны оси 0 х и, поскольку все точки волновой поверхности колеблются одинаково, смещение S будет зависеть только от координаты х и времени t

S = S (x, t). (6.2.2).

Рассмотрим некоторую частицу среды, находящуюся от источника колебаний О на расстоянии х. Пусть колебания точек, лежащих в плоскости х = 0 имеют вид

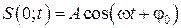. (6.2.3)

Найдем вид колебания точек в плоскости, соответствующей произвольному значению х. Для того, чтобы пройти путь от плоскости х = 0 до плоскости х, волне требуется время t = x /u. Следовательно, колебания частиц, лежащих в плоскости х, будут отставать по времени на t от колебаний частиц в плоскости х = 0 и описываться уравнением

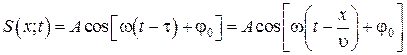. (6.2.4)

где А − амплитуда волны; j₀ − начальная фаза волны (определяется выбором начал отсчета х и t).

Зафиксируем какое-либо значение фазы 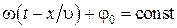. Это выражение определяет связь между временем t и тем местом х, в котором фаза имеет фиксированное значение. Продифференцировав данное выражение, получим

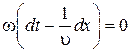Þ 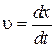. (6.2.5)

Таким образом, скорость распространения волны есть скорость перемещения фазы, и называется фазовой скоростью.

При u > 0 волна распространяется в сторону возрастания х. Волна, распространяющаяся в противоположном направлении, описывается уравнением

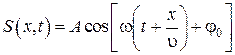. (6.2.6)

Придадим уравнению плоской волны симметричный относительно х и t вид. Для этого введем величину 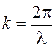, которая называется волновым числом, которое можно представить в виде

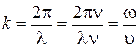. (6.2.7)

Тогда уравнение плоской волны будет иметь вид

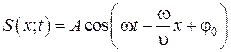Þ 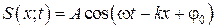. (6.2.8)

Мы предполагали, что амплитуда колебаний не зависит от х. Для плоской волны это наблюдается в том случае, когда энергия волны не поглощается средой. При распространении в поглощающей энергию среде интенсивность волны с удалением от источника колебаний постепенно уменьшается, т. е. наблюдается затухание волны. В однородной среде такое затухание происходит по экспоненциальному закону 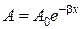. Тогда уравнение плоской волны для поглощающей среды имеет вид

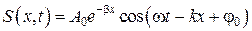. (6.2.9)

Дата добавления: 2014-01-07