Скорость распространения волн в различных средах

Для определения скорости упругих волн в упругой среде рассмотрим продольную плоскую волну, распространяющуюся в направлении оси 0 х. Выделим в среде цилиндрический объем с площадью основания S ₀ и высотой dx. Смещения S частиц с разными х в каждый момент времени оказываются различными. Если основание цилиндра с координатой х имеет в некоторый момент времени смещение S, то смещение основания с координатой x + dx будет S + dS. Тогда, рассматриваемый объем деформируется и получает удлинение dS или относительную деформацию e = ¶ S /¶ x (деформации растяжения). Наличие деформации свидетельствует о существовании нормального напряжения s, которое при малых деформациях пропорционального величине деформации. По закону Гука для деформации растяжения − сжатия

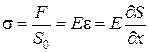, (6.4.1)

где Е − модуль Юнга среды.

Из зависимости смещения от координаты х видно, что относительная деформация ¶ S /¶ x, а также, и напряжение s в фиксированный момент времени зависят от х. В соответствии с этим, продольная волна состоит из чередующихся разрежений и сжатий среды.

Теперь для цилиндрического объема запишем уравнение движения. Масса этого объема

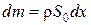. (6.4.2)

где r − плотность недеформированной среды.

Ввиду малости dx можно считать ускорение всех точек цилиндра одинаковым и равным

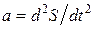. (6.4.3)

Тогда этот участок объема будет растянут под влиянием сил F ₁ и F ₂, приложенных к основаниям цилиндра в данный момент времени. Силы, действующие на левое и правое основание цилиндра равны, соответственно

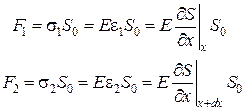. (6.4.4)

После разложения силы F ₂ в ряд, получим

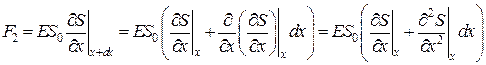, (6.4.5)

и результирующая F ₁, F ₂ сил, действующая на элемент объема равна

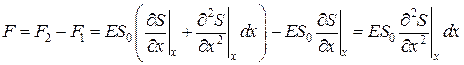. (6.4.6)

Используя основное уравнение динамики поступательного движения (2.1.2) и, подставив значения массы, ускорения и силы, получим

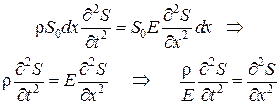. (6.4.7)

Из сравнения этого уравнения с волновым уравнением для плоской волны (6.3.6) 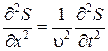, получим

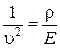Þ 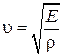, (6.4.8)

где Е − модуль Юнга.

Полученное уравнение определяет фазовую скорость продольных упругих волн.

Если проделать аналогичные преобразования для поперечных упругих волн, то фазовая скорость поперечных упругих волн будет иметь следующий вид

, (6.4.9)

где G − модуль сдвига.

Дата добавления: 2014-01-07