Сферические линзы

Сферические линзы в виде очков и лупы были известны еще в глубокой древности. В Ассирии и Вавилоне их делали из природных кристаллов – горного хрусталя и турмалина. Более сложные линзовые приборы – зрительная труба, телескоп, микроскоп – были созданы в начале 17 века благодаря научным открытиям Декарта, Галилея, Кеплера, Ньютона.

Термин линза в переводе с латинского означает «чечевица», которую по форме напоминала сама линза и которая является простейшей центрированной системой, состоящей всего из двух сферических преломляющих поверхностей, ограничивающих прозрачную среду, как правило, стекло или другой прозрачный материал с определенным показателем преломления n. При создании оптических приборов в основном используются осесимметричные линзы с общей осью симметрии бесконечного порядка для обеих поверхностей линзы (Рис.1).

Рис. 1. Отдельная линза в воздухе.

Конструктивными параметрами любой линзы являются:

r₁ – радиус кривизны первой сферической поверхности,

r₂ – радиус кривизны второй сферической поверхности,

d – толщина линзы по оси (О₁О₂),

D – диаметр линзы,

n – показатель преломления материала линзы.

Если одна из поверхностей линзы плоская, то она также рассматривается как сферическая с радиусом кривизны бесконечно большой величины – (∞).

На чертеже изображают линзу так, чтобы ход лучей был слева направо, т.е. нумерация поверхностей идет по ходу лучей света и условились поверхность линзы, расположенную на чертеже слева считать первой, а лежащую справа – второй, и обозначать центры кривизны поверхностей С₁ и С₂ а их радиусы соответственно r₁ и r₂. Прямая соединяющая центры сфер С₁ и С₂, называется главной оптической осью, а точки пересечения поверхностей линзы с главной оптической осью О₁ и О₂ – вершинами линзы. Таким образом, r₁ = О₁С₁, а r₂ = О₂С₂. Если центр сферы находится справа от вершины поверхности, то радиус ее считается положительным, а если наоборот – отрицательным.

Часть пространства, расположенная слева от первой поверхности линзы, называется пространством предметов, а другая часть, расположенная справа от последней поверхности – пространством изображений.

Все линзы можно подразделить на шесть основных типов, а типы объединить в два больших класса, по три в каждом (Рис.2).

· Положительные, или собирательные линзы:

двояковыпуклые, плосковыпуклые, положительные мениски (вогнуто – выпуклые),

· Отрицательные, или рассеивающие линзы:

двояковогнутые, плосковогнутые, отрицательные мениски (выпукло - вогнутые)

Положительные линзы, преломляя отдельные лучи проходящих через линзу световых пучков, отклоняют их в направлении к среднему лучу пучка, т.е. собирают пучки.

Отрицательные линзы, наоборот, – отклоняют лучи пучков в сторону от среднего луча, т. е. рассеивают световые пучки.

Формально положительные и отрицательные линзы различаются по толщине в центре и на краю. У всех положительных линз средина всегда толще чем края, у отрицательных - наоборот. Но принципиальным различием является знак заднего фокусного расстояния. Если заднее фокусное расстояние имеет знак плюс, то линза положительная, если минус – то отрицательная.

Рис. 2. Основные типы сферических линз:

1-двояковыпуклая, 2-плосковыпуклая, 3-мениск вогнуто-выпуклый,

4-двояковогнутая, 5-плосковогнутая, мениск выпукло-вогнутый.

Рассмотрим кардинальные (главные) точки, линии, плоскости и отрезки для случая тонкой линзы (Рис.1, Рис. 3).

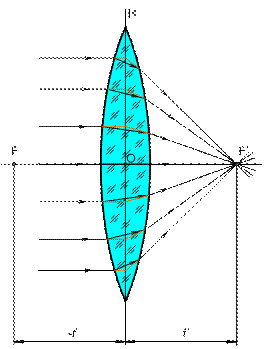
Рис. 3. Преломление пучка параллельных лучей в линзе.

Главная оптическая ось – это прямая, соединяющая центры кривизны поверхностей, образующих линзу, т.е. центры сфер С₁ и С₂. Точки же пересечения поверхностей линзы с главной оптической осью О₁ и О₂ называют вершинами линзы.

Задний главный фокус (F^') – это точка на главной оптической оси, в которой после преломления в линзе пересекутся все лучи параллельные главной оптической оси, идущие слева направо из пространства предметов в пространство изображений.

Передний главный фокус (F) – это точка на главной оптической оси, в которой после преломления в линзе пересекутся все лучи параллельные главной оптической оси, идущие справа налево из пространства изображений в пространство предметов.

Передняя и задняя фокальные плоскости – плоскости перпендикулярные главной оптической оси и проходящие, соответственно, через точки переднего и заднего фокусов. Наклонные по отношению к оси параллельные пучки лучей также будут сходится в точки, но уже вне оси, а поверхность, проведенная через эти фокусы наклонных световых пучков, как раз и является фокальной поверхностью. Иными словами, фокальная поверхность – это геометрическое место фокусов. В идеальных оптических системах фокальная поверхность плоская.

Оптический центр тонкой линзы О - единственная точка, через которую лучи проходят не преломляясь. Побочные оптические оси – лучи которые проходят через оптический центр О линзы и, конечно, мимо центров кривизны линзы.

Главная оптическая плоскость Н - плоскость проведенная через оптический центр линзы перпендикулярно главной оптической оси. Т.е. это условная поверхность, на которой происходит преломление светового пучка, проходящего через линзу. Точка пересечения главной оптической плоскости с главной оптической осью называется главной точкой линзы.

Главное фокусное расстояние – это расстояние между главной плоскостью и фокальной плоскостью линзы. Этот отрезок является основной характеристикой линзы. Причем, если это расстояние от главной точки линзы до точки заднего фокуса, то оно называется задним фокусным расстоянием и обозначается ƒ' (Рис.3, отрезок ОF^'), а если это расстояние от главной точки линзы до точки переднего фокуса, то оно называется передним фокусным расстоянием и обзначается ƒ (отрезок OF). Для линзы, находящейся в однородной среде (например, воздух), переднее и заднее фокусные расстояния будут одинаковы по абсолютной величине и противоположны по знаку‌‌ ‌ │-ƒ‌‌ │ = ƒ'. Т.е., если фокусное расстояние отсчитывается от главной точки вправо, то оно считается положительным, а если влево – то отрицательным: Если слева от линзы будет вода, а справа – воздух, то переднее фокусное расстояние численно будет равно – ƒ, а заднее – nƒ, где n –показатель преломления воды.

Величина фокусного расстояния характеризует преломляющую способность линзы и позволяет точно определить размер получаемого изображения. Вместо величины фокусного расстояния иногда для характеристики преломляющей способности пользуются величиной, обратной фокусному расстоянию. Эта величина называется оптической силой линзы и обозначается буквой Ф. В общем случае:

Ф=- n₁/ ƒ= n₃/ ƒ',

где n₁ и n₃ –показатели преломления сред до и после линзы.

Если линза находится в воздухе, то n₁ = n₃ = 1, а Ф= - 1/ ƒ = 1/ ƒ' и чем меньше фокусное расстояние, тем она сильнее преломляет лучи (отсюда и название – сила линзы). Единицей оптической силы является диоптрия. Фокусному расстоянию в 1 метр соответствует оптическая сила 1 диоптрия, а, например: при ƒ=100 мм – Ф=10 дптр., при Ф=-20 дптр. – ƒ=-50 мм и т.д. Если рассчитывать фокусное расстояние толстой, реальной линзы при известных радиусах кривизны, толщине линзы и показателе преломления ее материала, то необходимо использовать следующую формулу:

ƒ'= nr₁r₂/ (n-1)[ n(r₁-r₂ )+(n-1) d].

Для тонкой же линзы (ее еще называют бесконечно тонкой или идеальной линзой), в которой толщина линзы существенно мала по сравнению с радиусами кривизны ее преломляющих поверхностей, т.е. при d=0 формула для определения фокусного расстояния упрощается:

ƒ'= r₁r₂/ (n-1)(r₁-r₂ ).

На практике чаще всего пользуются приближенными формулами для идеальной линзы, ибо ошибка составляет около 1%.

Т.е. тонкую (идеальную) линзу можно представить в виде виртуального оптического элемента, состоящего из двух фокальных поверхностей, между которыми размещена главная плоскость, обладающая собирающей или рассеивающей способностью. Реальные линзы и объективы имеют как бы две главные плоскости – переднюю Н и заднюю Н', линейное увеличение между которыми равно плюс единице.

Рассмотрим графическое построение изображений, создаваемых положительной линзой при различном расположении предмета относительно линзы. На чертежах часто намечают т. н. точки двойного фокуса 2F, хотя для построения изображения двойной фокус принципиального значения не имеют. Это только позволяет проанализировать различные случаи размещения предмета относительно линзы.

При построении изображения создаваемого сферическими линзами и зеркалами необходимо воспользоваться тремя лучами, ход которых заранее известен:

- луч, идущий паралельно оптической оси линзы, который после преломления пройдет через точку заднего фокуса;

- наклонный луч, проходящий через точку переднего фокуса линзы, который после преломления пройдет паралельно оптической оси;

- луч, проходящий через главную точку линзы, не преломляется линзой. Возможно лишь его смещение на расстояние между передней и задней главными точками при использовании в построении передней и задней главных плоскостей.

Рассмотрим шесть случаев построения изображения положительными линзами.

Случай 1: Расстояние от предмета до линзы а = ∞ (Рис. 4). В этом случае считается, что лучи идут параллельно главной оптической оси и пересекаются в точке заднего главного фокуса F'. В фото-, кино- и телевизионных съемочных объективах для получения такого случая дистанционную шкалу необходимо установить на отметку «бесконечность» (∞).

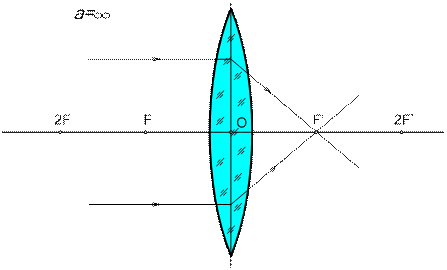
Рис. 4. Построение изображения при размещении предмета

на расстоянии от линзы а = ∞.

Случай 2: ∞ > a > 2ƒ – предмет АВ расположен за двойным фокусным расстоянием перед линзой (Рис. 5). Его изображение А'В' получится за задним фокусом линзы и будет действительным, уменьшенным и перевернутым. Этот случай характерен для практики съемок и чтобы получить резкое изображение в кадровом окне или на ПЗС-матрице, оптический блок объектива выдвигается с помощью кольца шкалы дистанций.

Рис. 5. Построение изображения при размещении предмета

на расстоянии от линзы ∞ > a > 2ƒ.

Случай 3: a = 2ƒ – предмет АВ расположен на двойном фокусном расстоянии перед линзой (Рис. 6). Его изображение А'В' получится также на двойном фокусном расстоянии за линзой и будет действительным, перевернутым и равным по величине предмету. Этот случай характерен для режима макросъемок и при репродуцировании для получения точной копии, но так как требуется значительное выдвижение объектива, то используются дополнительные еще и удлинительные кольца.

Рис. 6. Построение изображения при размещении предмета

на расстоянии от линзы a = 2ƒ.

Случай 4: 2f > a > f – при этом предмет АВ расположен на расстоянии больше фокусного, но меньше двойного фокусного перед линзой. Его изображение А'В' будет находиться за двойным фокусным расстоянием линзы и будет действительным, увеличенным, перевернутым. Таким образом, по мере приближения предмета к линзе, размер действительного изображения, даваемого линзой, увеличивается (Рис. 7). Такое изображение необходимо получить при макросъемке, когда требуется увеличение объекта съемки. Но чаще всего этот случай используется при проекции, где объектом является кадр на кинопленке.

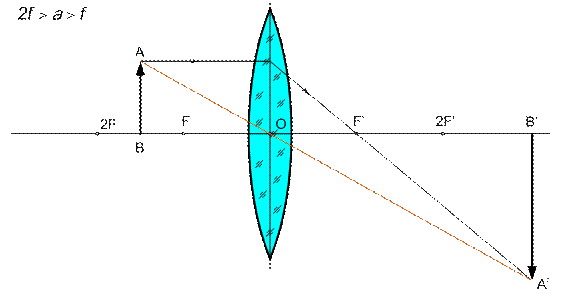
Рис. 7. Построение изображения при размещении предмета

на расстоянии от линзы 2f > a > f.

Случай 5: a = f – в этом случае предмет АВ находится в точке фокуса линзы, лучи после преломления в ней пойдут параллельным пучком, т. е. изображение будет располагаться в бесконечности (Рис. 8).

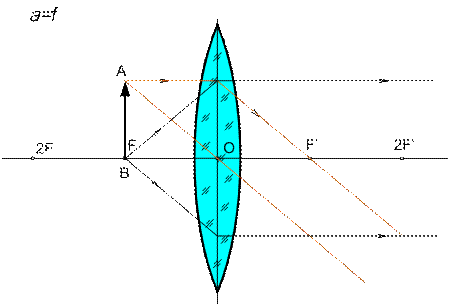
Рис. 8. Построение изображения при размещении предмета

на расстоянии от линзы a = f.

На основании этого случая построен прибор, который создает параллельный пучок (коллимирует) и поэтому называется коллиматором, и используется при исследовании объективов и при определении его некоторых оптических параметров.

Случай 6: a < f – предмет АВ находится между линзой и фокусом, лучи после преломления пойдут расходящимся пучком (Рис. 9). Это значит, что изображение А'В' - мнимое. Для его построения следует продлить до пересечения преломленные линзой лучи в обратном направлении. Изображение – увеличенное, прямое и расположено в пространстве предметов.

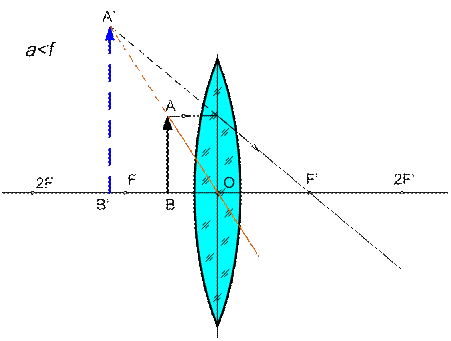
Рис. 9. Построение изображения при размещении предмета

на расстоянии от линзы a < f.

Однако, мы используем на практике и этот случай, когда работаем с лупой. Лупа дает мнимое прямое и увеличенное изображение и предназначена для рассматривания глазом мелких предметов. Лупой называется короткофокусная линза с f от 10мм до 100 мм для получения увеличенных изображений. Увеличение лупы равно отношению расстояния наилучшего зрения к фокусному расстоянию лупы 250мм/f_лупы.

Методика построения изображения отрицательными линзами аналогична методике построения положительными линзами, как это было показано выше.

При построении изображения, даваемого отрицательной линзой (рис.10) следует иметь в виду, что переднее фокусное расстояние линзы имеет положительное значение, а заднее - отрицательное. Независимо от места расположения предмета относительно отрицательной линзы изображение всегда будет уменьшенным, мнимым и прямым.

Рис. 10. Построение изображения отрицательными линзами.

Как правило, отрицательные линзы входят в состав оптических схем объективов, окуляров, но и используютя в качестве разнообразных оптических насадок.

Дата добавления: 2014-01-07