Запись уравнений связи в координатной форме

Число степеней свободы движения

Обобщенные координаты в неголономных системах.

1º. Условия, накладываемые на математические модели связей в неголономных системах

Неголономные механические системы с линейными кинематическими связями описываются следующими уравнениями

, , (2.5.1)

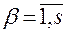, . (2.5.2)

Считаем, что все интегрируемые связи проинтегрированы и вошли в первую группу уравнений, т.е. вторая группа содержит только неинтегрируемые дифференциальные связи. Причем вторая группа уравнений обязательно присутствует.

В обозначениях, принятых в §4 для вектора-столбца 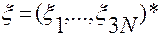, составленного из координат точек механической системы

,..., ,

система уравнений (2.5.1), (2.5.2) примет вид (сохраняем за ней ту же нумерацию):

, , (2.5.1)

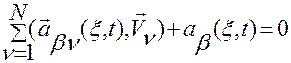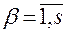, . (2.5.2)

1.2. Требования, предъявляемые к уравнениям
геометрических связей

Как и в §4, требуем, чтобы уравнения голономных связей удовлетворяли условиям, сформулированным в этом параграфе:

а) ;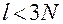

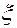б) функции , — определены и дважды непрерывно дифференцируемы по совокупности переменных и 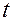из области ;

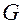в) 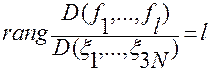при любых значениях .

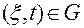1.3. Требования, предъявляемые к уравнениям
кинематических (неинтегрируемых) связей

На кинематические связи (2.5.2) дополнительно накладываем следующие условия.

1. 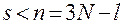, т.е. общее количество связей (голономных и неголономных) должно быть меньше .

2. Функции и 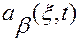, , 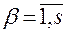определены и непрерывно дифференцируемы по совокупности переменных 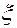и 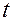из области .

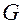3. Прежде чем сформулировать третье условие, составим матрицу 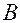размерности 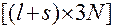. Представим ее в блочном виде

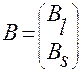, (2.5.3)

где — матрица размерности , совпадающая с матрицей Якоби, составленной по переменным 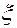от функций , ; 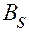— матрица коэффициентов при скоростях в уравнениях (2.5.2).

Матрица определяется формулой (2.4.2) §4

. (2.4.2)

Матрица 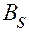имеет вид

. (2.5.4)

В (2.5.4) введены обозначения:

, , ,

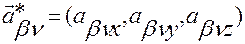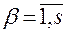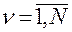— координаты вектора в заданной системе отсчета.

Тогда последнее условие (условие 3), накладываемое на кинематические связи, состоит в требовании, чтобы

(2.5.5)

при всех .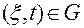

Поясним смысл условия 3.

Для этого определим, какие ограничения на скорости точек неголономной механической системы накладываются всеми ее связями.

1.4. Ограничения на скорости, накладываемые связями
в неголономных системах

Перейдем от уравнений связи (2.5.1) к их дифференциальной форме и присоединим к ним уравнения кинематических связей. Придем к следующей системе уравнений дифференциальных связей

, , (2.5.6)

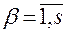, . (2.5.7)

Легко видеть, что матрица 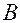, имеющая вид (2.5.3)

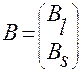, (2.5.3)

совпадает с матрицей коэффициентов при скоростях в системе (2.5.6), (2.5.7).

Ясно, что каждое уравнение системы (2.5.6), (2.5.7) при любых фиксированных положениях 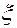в моменты времени 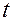из области 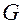задает ограничения на скорости механической системы, которые она может иметь в эти моменты времени в указанных положениях.

Следовательно, механическая система может иметь в положении, которое она занимает в момент времени 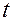, только такие скорости, которые являются решениями совместной системы уравнений (2.5.6), (2.5.7).

Из вида системы уравнений (2.5.6), (2.5.7) легко устанавливается смысл условия 3, о котором говорится в пункте 1.3.

А именно, согласно теореме об условиях независимости функций (см. §4, п.1º), равенство (2.5.5)

(2.5.5)

означает независимость функций, задающих левые части равенств (2.5.6), (2.5.7).

В этих функциях в качестве аргументов выступают скорости механической системы, а ее положения и время рассматриваются как параметры.

Следовательно, условие 3 обеспечивает выполнение требования, чтобы ограничения, которые накладываются на скорости точек механической системы при совместном действии голономных и кинематических связей в любой момент времени 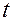в любом положении, допускаемом голономными связями (2.5.1)

, , (2.5.1)

были независимыми.

Дата добавления: 2014-01-07