Определение 2. Число называется числом степеней свободы движениянеголономной механической системы

Число 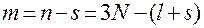называется числом степеней свободы движениянеголономной механической системы.

Из уравнений (2.5.6), (2.5.7) и условия (2.5.5)

, , (2.5.6)

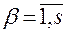, , (2.5.7)

. (2.5.5)

можно сделать следующий вывод:

число 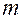задает количество независимых компонент скоростей точек, входящих в состав неголономной механической системы.

Действительно, из уравнений (2.5.6), (2.5.7) при выполнении условия (2.5.5), согласно теореме о неявных функциях, можно выразить компонент скоростей через 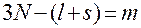оставшихся независимых компонент этих скоростей.

Если неголономные связи отсутствуют, т.е. механическая система является голономной, то отсутствуют уравнения (2.5.7)

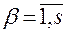, . (2.5.7)

А тогда из системы (2.5.6)

, , (2.5.6)

можем выразить 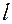компонент скоростей 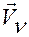, , точек, входящих в состав голономной механической системы. Эти компоненты будут выражаться через 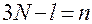остальных независимых компонент.

В таком случае, если распространим понятие числа степеней свободы движения и на голономные системы, то будем иметь:

,

т.е. вголономных системах число степеней свободы движения 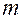совпадает с числом степеней свободы положения .

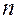Иначе говоря, в голономных системах количество независимых координат положения механической системы и число независимых компонент скоростей совпадают.

Что касается неголономных систем, то для них всегда имеет место неравенство

.

§6. Обобщенные скорости и ускорения.
Основные кинематические соотношения Лагранжа

1º. Обобщенные скорости и ускорения и их связь
со скоростями и ускорениями точек механической системы

Пусть задано движение механической системы 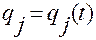, , через обобщенные координаты.

Дата добавления: 2014-01-07