Достаточность. Пусть . Предположим противное, что столбцы матрицы линейно зависимы

Пусть 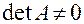. Предположим противное, что столбцы матрицы 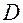линейно зависимы. Тогда существует вектор 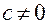размерности 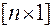такой, что

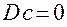. (2.6.9)

После умножения равенства (2.6.9) на 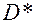слева, получим

.

Отсюда следует, что вектор 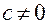является решением однородной системы уравнений.

Матрица коэффициентов этой системы совпадает с матрицей 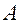, которая имеет 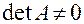. А это означает, что такая система может иметь только нулевое решение .

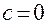Пришли к противоречию с условием 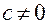. Лемма доказана.

1.3. Зависимость обобщенных скоростей и обобщенных
ускорений от скоростей и ускорений точек
механической системы

Вернемся к равенствам (2.6.5)

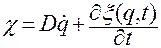. (2.6.5)

Они справедливы на любых движениях и любых положениях механической системы.

Умножая равенства (2.6.5) на 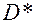слева, получаем

.

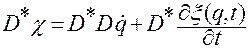Учитывая условие (2.6.6)

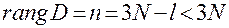(2.6.6)

и утверждение леммы (из условия (2.6.6) следует, что столбцы матрицы 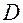линейно независимы; из леммы следует тогда, что матрица 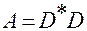неособая при любых 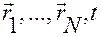), находим

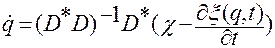. (2.6.10)

Если в матрице 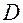и в векторе 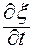аргумент 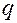заменить обратной функцией 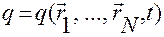, получаемой из соотношений (2.6.1), то формула (2.6.10) даст однозначную зависимость обобщенных скоростей 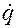от скоростей 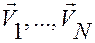на любом положении 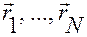механической системы в любой момент времени .

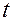Поэтому из (2.6.10) можно сделать вывод:

обобщенные скорости на любых движениях и в любых положениях однозначно связаны со скоростями механической системы.

Объединяя теперь равенства (2.6.5) и (2.6.10)

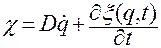, (2.6.5)

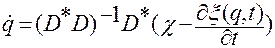, (2.6.10)

приходим к следующему заключению относительно связи между скоростью 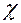и обобщенными скоростями механической системы:

между скоростью 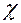и обобщенными скоростями 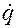механической системы в любых ее положениях существует взаимно однозначное соответствие, определяемое формулами ( 2.6. 5) и ( 2.6. 10).

Аналогичным путем из (2.6.4)

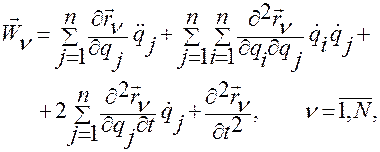(2.6.4)

получаем

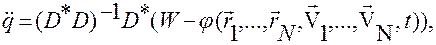(2.6.11)

где 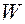и 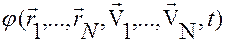обозначают векторы-столбцы размерности 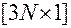, составленные из компонент 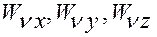ускорений 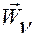и компонент 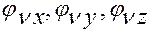вектор-функций 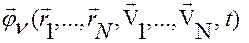, , 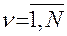соответственно.

Функции 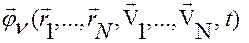строятся по функциям 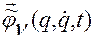, которые имеют вид

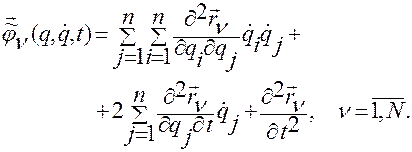(2.6.12)

Чтобы получить 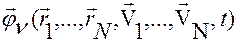, необходимо в (2.6.12) заменить аргументы 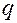на 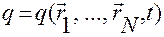, а обобщенные скорости 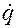— на их зависимость от 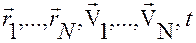, найденную по формулам (2.6.10).

Обобщая сказанное, можем утверждать, что соотношения (2.6.1), (2.6.3), (2.6.4)

, , (2.6.1)

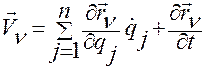, , (2.6.3)

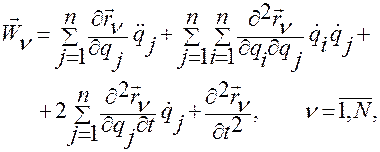(2.6.4)

дают прямые зависимости положений, скоростей и ускорений от обобщенных координат, обобщенных скоростей и обобщенных ускорений.

На них можно смотреть как аналитические зависимости положений, скоростей и ускорений механической системы, однозначно разрешимые относительно обобщенных координат, обобщенных скоростей и обобщенных ускорений.

Обратная зависимость обобщенных скоростей и обобщенных ускорений от скорости 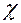и ускорения 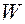механической системы задается соотношениями (2.6.10) и (2.6.11), соответственно:

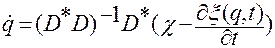, (2.6.10)

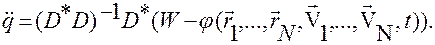(2.6.11)

2º. Кинематическая лемма Лагранжа

Для функций (2.6.1), (2.6.3):

, , (2.6.1)

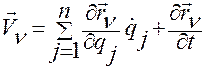, , (2.6.3)

на любых движениях механической системы справедлива следующая кинематическая лемма Лагранжа.

Дата добавления: 2014-01-07