Лемма Лагранжа

На любых движениях механической системы справедливы следующие соотношения:

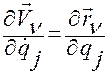, , , (2.6.13)

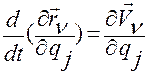, , . (2.6.14)

В левой части равенства (2.6.14) выражение 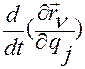обозначает полную производную по времени 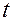от вектор-функции 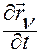вдоль движения механической системы (см. гл.1, §5, п.8º, определение 11).

Равенства (2.6.13) и (2.6.14) называются основными кинематическими соотношениями Лагранжа при дифференцировании функци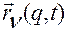й и 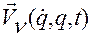, задаваемых формулами (2.6.1) и (2.6.3), соответственно.

Доказательство этой леммы дословно повторяет доказательство аналогичных утверждений, содержащихся в лемме Лагранжа в главе 1, §5, п.8º.

3º. Ограничения, накладываемые голономными связями
на обобщенные координаты и обобщенные скорости

В этом пункте дадим ответ на вопрос, какие ограничения на обобщенные координаты и обобщенные скорости накладывают связи в голономных механических системах.

Ответ на этот вопрос следует искать в тех требованиях, которые предъявляются к обобщенным координатам при их выборе для описания движений механических систем, а также в условиях, которым должны удовлетворять математические модели связей в таких системах.

3.1. Отсутствие ограничений на изменения
обобщенных координат

Согласно определению обобщенных координат голономных механических систем и условий, которые накладываются на выбор обобщенных координат, можно записать следующее.

Подстановка в уравнения геометрических связей

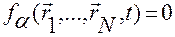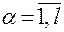, , (2.6.15)

функций 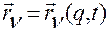, , задающих связь обобщенных координат 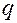и положений точек механической системы, обращают равенства (2.6.15) в тождества по 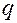и :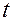

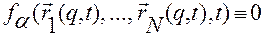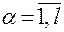, . (2.6.16)

Тождества (2.6.16) будут справедливы для функций 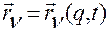, , соответствующих любому выбору переменных 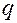, который позволяют сделать уравнения связей (2.6.15).

Из этого свойства следует вывод 1.

Дата добавления: 2014-01-07