Вывод 1

При любом выборе обобщенных координат, который допускают геометрические связи (2.6.15), уравнения связей не накладывают никаких ограничений на значения этих координат.

3.2.. Отсутствие ограничений голономными связями
на изменения обобщенных скоростей.

Проверим теперь, будут ли уравнения голономных связей накладывать ограничения на значения обобщенных скоростей .

В соответствии с ранее сделанными выводами (см. §2, п.1º) эти уравнения действительно накладывают ограничения на скорости .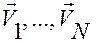

Они имеют вид (задаются уравнениями (2.2.5) из §2, п.1º):

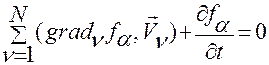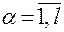, . (2.6.17)

Подставим зависимость 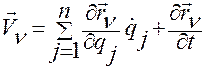(2.6.3)

, , (2.6.3)

скоростей 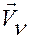, , 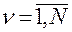от обобщенных скоростей 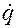в ограничения (2.6.17). Придем к равенствам

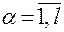, , (2.6.18)

в которых

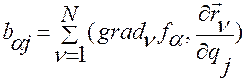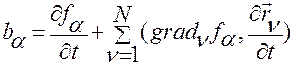, . (2.6.19)

Покажем, что

при любых , , , ,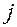

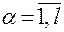и

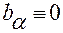при любых .

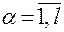Продифференцируем тождества (2.6.16)

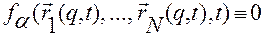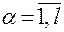, , (2.6.16)

по , , и по 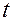при любых , 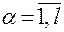. Получим

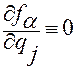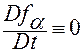, . (2.6.20)

Раскрывая левую часть тождеств (2.6.20) и сравнивая с (2.6.19), можем записать

, ,

.

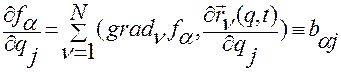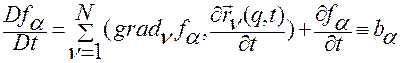Учитывая (2.6.20), приходим к требуемым тождествам:

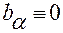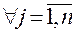, для и .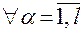

Отсюда делаем вывод 2.

Дата добавления: 2014-01-07