Лекция 1. Понятие о тензорах. Скаляры. Векторы. Псевдовекторы. Тензоры и их преобразования

Физические величины, не зависящие от направления, называются скалярными. Аналитически скалярные величины задаются одним числом. Следует различать два вида скалярных величин: истинно скаляры и псевдоскаляры. Различие между скалярами и псевдоскалярами состоит в том, что первые из них «нечувствительны» к изменению знака системы координат изменяют свой знак. Эта способность псевдоскаляров изменять знак при изменении знака системы координат означает, что каж­дый псевдоскаляр является либо правым (ему в этом случае можно приписать знак плюс), либо левым (имеющим знак минус). Изменение знака псевдоскаляра в этом случае есть только резуль­тат изменения знака системы. Сам по себе псевдоскаляр, конечно, при изменении знака системы координат не меняется.

«Нечувствительность» скаляров к изменению знака при изме­нении знака системы координат не лишает их возможности быть как положительными, так и отрицательными. Так, например, гидростатическое растяжение сре­ды может характеризоваться зна­ком плюс, а сжатие — знаком минус. В свою очередь, оптичес­кая активность некоторых сред характеризуется псевдоскаляром и может быть положительной (на­пример, вращение плоскости поля­ризации по правому винту) или отрицательной (вращение по ле­вому винту). Ниже скаляры и псевдоскаляры будут обозначаться строчными (а, b,...) и пропис­ными (А, В,..) буквами соответственно.

Простейшими направленными величинами являются векторы. Направленность векторных величин состоит в том, что у них можно различить противоположные концы. Имеется два вида векторных величин: векторы полярные (или просто векторы) и векторы аксиаль­ные (осевые), В полярных векторах различие концов носит ска­лярный характер: их противоположные концы можно характери­зовать скалярами, имеющими одинаковую абсолютную величину, но противоположные знаки. Аналогично аксиальные векторы могут характеризоваться псевдоскалярами противоположных знаков: один из них является правым (скажем, положительным), а другой — левым (скажем, отрицательным). Физики часто стал­киваются с векторными величинами. Так, например, сила и напря­женность электрического поля определяются полярными векто­рами, а такие величины, как момент количества движения и напря­женность магнитного поля,— аксиальными векторами.

Если компоненты некоторого полярного вектора а в исходной системе координат X, У, Z обозначить (i = 1, 2, 3), то при переходе к новой системе координат Z', Y', Ъ' (рис. 21), определяемом матрицей направляющих косинусов (i, j=1,2,3)

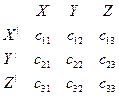(1.1)

новые компоненты вектора будут 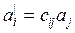. (1.2)

Переход от новых компонент к старым осуществится с помощью формулы

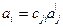. (1.3)

При операциях симметрии второго рода (зеркальных поворотах) формулы преобразования имеют вид

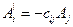; (1.4)

Наличие знака минус в формулах (1.4) обусловлено тем, что концы аксиального вектора «чувствительны» к изменению знака системы координат.

Следующими по сложности направленными величинами являются тензоры второго ранга. Полярные тензоры второго ранга определяют линейную связь между компонентами двух полярных или двух аксиальных векторов, а аксиальные – полярного и аксиального векторов. Полярный тензор 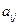, связывающий компоненты полярных векторов P и Q, определяется девятью компонентами.

Аксиальным тензором второго ранга описывается, например, поляризация кристалла Р в зависимости от магнитного поля Н,

(1.6)

а также намагничивание кристалла в результате его поляризации (магнитоэлектрический эффект). Компоненты аксиального тен­зора будут обозначаться 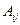. Формулы преобразования компонент тензоров второго ранга (а также скаляров и векторов) приведены в табл. 1.1. Необходимо обратить внимание на то, что в формулах преобразования аксиального тензора при операциях второго рода (зеркальных поворотах) берется знак минус. Это опять свя­зано с тем, что аксиальные величины чувствительны к изменению знака системы координат, т. е. являются правыми или левыми.

Можно рассмотреть и тензоры более высокого ранга. Так, тен­зоры третьего ранга будут описывать связь между векторами и тензорами второго ранга. Такие тензоры будут иметь компонент. Тензорами третьего ранга, например, описы­вается пьезоэлектрический эффект в кристаллах. Тензоры чет­вертого ранга описывают связь двух тензоров второго ранга и имеют компоненту и т.д. В общем случае число компонент тензора, имеющего ранг n, равно 3ⁿ. Полагаяи 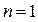, получаем число компонент 1 и 3. Отсюда следует возможность трактовать скаляры как тензоры нулевого ранга, а векторы – как тензоры первого ранга.

Полярный тензор второго ранга общего вида, имеющий девять различных компонент, может быть представлен (в соответствии с правилами тензорной алгебры) в виде суммы двух тензоров:

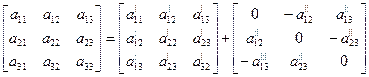, (1.6)

первый из которых , является симметричным, а второй 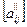- антисиммет- ричным.

Симметричным называется тензор, компоненты которого удовлетворяют условию , антисимметричным – условию .

Из тензорной алгебры также известно, что для любого симметричного тензора может быть найдена система координат, в которой он будет иметь только диагональные компоненты. Такой тензор называется приведенным к диагональному виду, а система координат, в которой он имеет этот вид, называется главной. Система координат, в которой антисимметричный тензор записывается в простейшем виде, называется также главной системой, а ось с нулевыми компонентами – главной осью.

Наибольший интерес представляют следующие частные формы аксиального тензора второго ранга:

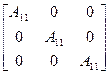; (1.7)

Тензор (1.7) (по соображениям, только что изложенным для скаляра) определяет псевдоскаляр. Антисимметричный аксиальный тензор типа (1.7) определяет полярный вектор.

Таблица 1.1.

Формулы преобразования компонент скаляров, векторов и тензоров второго ранга

Величина	Ранг тензора	Число независимых компонент	Формулы преобразования
при преобразованиях системы координат без изменения знака	при преобразованиях системы координат с изменением знака
Скаляр   Псевдоскаляр			a^|=a a=a^| A^|=A A=A^|	a^|=a a=a^| A^|= - A A= - A^|
Полярный вектор   Аксиальный вектор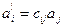
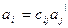
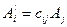
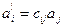
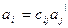
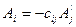
Полярный тензор второго ранга   Аксиальный тензор второго ранга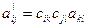

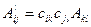
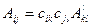
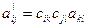
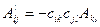
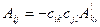
Симметрия скаляров. При определении симметрии скаляров, векторов и тензоров мы сталкиваемся впервые с величинами, геометрический образ которых нам может быть и неизвестен. Для тензоров понятие симметрии конкретизируется: симметрия тензоров есть их свой­ство быть инвариантными по отношению к преобразованиям системы координат (поворотам и зеркальным поворотам), в кото­рой они записаны. Тензоры, по определению, обладают теми или иными элементами и симметрии, если при преобразованиях системы координат, соответствующих этим элементам симметрии, все их компоненты преобразуются в себя. Практически это осущест­вляется путем преобразования системы координат, соответствую­щего искомому элементу симметрии, с последующим вычислением компонент тензора (вектора, скаляра) в новой системе с примене­нием соответствующих формул преобразования компонент.

Матрица косинусов, отвечающая операции инверсии системы координат в ее начале, имеет вид

(1.8)

В новой системе координат скаляр имеет тот же вид, что и в исходной, а это т означает, что скаляр имеет центр симметрии.

Покажем, что для скаляра

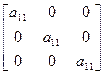(1.9)

все оси, проходящие через начало координат, являются осями симметрии бесконечного порядка и что любые плоскости, проходящие через начало системы координат, являются плоскостями симметрии тензора.

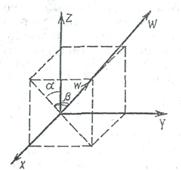
Рис.1.1. Последовательность поворотов системы координат, приводящая к повороту вокруг произвольного направления W

Проверим наличие осей симметрии в скаляре. Двумя поворотами (рис.1.1) сначала вокруг оси Y на угол 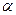, а затем вокруг оси X^| на угол 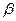совместим ось Z с осью W. Если после поворота системы координат компоненты тензора (1.9) преобразуются в себя, то это и будет означать, что ось W является осью скаляра. Повороту вокруг оси Y на произвольный угол 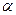соответствует матрица, косинусы которой равны

. (1.10)

Используя данные табл.1.1, получаем:

.

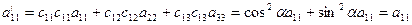Аналогично , . Все остальные коэффициенты при других преобразованиях системы координат скаляра, оказываются равными нулю.

Поворот новой системы координат X^|, Y^|, Z^| вокруг оси X^| на угол 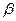описывается матрицей косинусов

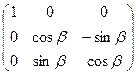, (1.11)

с помощью которой также получаем , . Любая ось, проходящая через начало координат, является осью симметрии бесконечного порядка

для скаляра.

Покажем теперь, что плоскость, перпендикулярная к оси , является плоскостью симметрии. Матрица косинусов, описываю­щая отражение системы координат Х", Y',Z" в этой плоскости, имеет вид

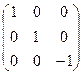(1.12)

Использование этой матрицы и табл. 1.1 приводит к следующему результату: , . Плоскость, перпенди­кулярная к оси W, оказывается, таким образом, плоскостью сим­метрии. В силу того, что W есть произвольное направление, любая плоскость, проходящая через начало координат, является плоскостью симметрии скаляра. Заметим, что оси являются не только простыми (поворотными) осями скаляра, но одновременно и зеркальными. Доказательство этого очевидно. Других элементов симметрии скаляр не имеет. Перечень основных элементов сим­метрии скаляра может быть записан в виде 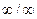, m, с.

Это следует понимать так: скаляр имеет бесконечное число осей сим­метрии (то, что они направлены друг к другу под любым углом, указывается записью двух символов через косую черту), беско­нечное число перпендикулярных (а в силу бесконечного числа' осей и продольных) к указанным осям плоскостей симметрии и центр симметрии. Группа симметрии скаляра, поэтому может быть обозначена как. Этот символ показывает, что каждое из направлений скаляра имеет ось симметрии , беско­нечное число продольных плоскостей симметрии и перпендику­лярную к этому направлению плоскость симметрии, т. е. имеет сим­метрию неподвижного цилиндра.

Для псевдоскаляра

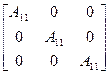(1.13)

как показывает аналитическое рассмотрение, так же, как и для скаляра, любая ось, проходящая через начало координат, является осью симметрии . Доказывать это нет необходимости, так как формулы преобразования компонент псевдоскаляра при простых поворотах совпадают с формулами преобразования компонент скаляра (см. табл. 1.1), а при нахождении осей в скалярах исполь­зовались только простые повороты системы координат.

Можно показать, что псевдоскаляр вовсе не имеет в качестве элементов симметрии плоскостей симметрии. Действительно, отра­жая систему координат Х', У ", Z" в этом случае в плоскости, пер­пендикулярной к оси W, получаем с использованием данных табл. 1.1: 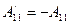, , .Таким образом, все компоненты псевдоскаляра принимают при этой операции новые значения, что свидетельствует о том, что рассматриваемая плоскость не является плоскостью симметрии. Так как направление W выбрано произвольно, ни одна из плоскостей, проходящих через начало, не будет плоскостью симметрии псевдоскаляра.

Псевдоскаляр не имеет также центра симметрии.

Каждое направление в псевдоскаляре имеет ось симметрии . Помимо этого оно также имеет бесконечное число осей симметрии второго порядка 2, перпендикулярных к этому направлению. Здесь пока что важно подчеркнуть именно это обстоятельство. Наличие осей 2 следует из того, что ось группы 2 является подгруппой . Поскольку же любое направление в псевдоскаляре является осью , конкретно выбранное направление имеет бесконечное число перпендикулярных к нему осей 2. Группа симметрии псевдоскаляра, таким образом, может быть записана символами .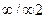

Симметрия векторов. Симметрию полярного вектора можно установить, рассматри­вая преобразование его компонент при преобразованиях системы координат. Сделать это довольно просто, поэтому для установления симметрии полярного вектора рассмотрим для разнообразия его геометрический образ.

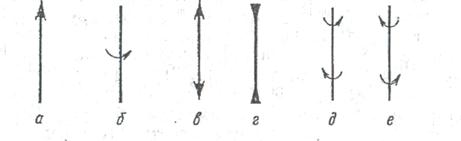
Рис.1.2. Графическое изображение векторов и простейших тензоров, отображающее их симметрию: а) – полярный вектор; б) – аксиальный вектор; в, г – простейшие полярные тензоры; д, е – простейшие правый и левый аксиальные тензоры

Поляр­ный вектор графически обычно представляется в виде отрезка прямой со стрелкой (рис.1.2,а). Его симметрия совпадает с сим­метрией полярного направления; полярный вектор имеет симметрию неподвижного конуса. Ось вектора является осью симметрии . Полярный вектор имеет бесконечное число плоскостей симметрии т, проходящих через ось . Покажем, что такими же элементами симметрии обладает и антисимметрич­ный аксиальный тензор

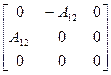(1.14)

Здесь уместно сделать важное замечание. Естественно, что симметрия конкретного тензора не зависит от системы координат, в которой мы его записываем. Тензоры, имеющие другие отличные от нуля недиагональные коэффициенты, также определяют собой полярный, вектор, но при такой записи не так просто найти их элементы симметрии. Другими словами, симметрия того или иного тензора есть его внутреннее свойство, не зависящее от выбора системы координат. Эта внутренняя харак­теристика наиболее четко и наглядно выявляется в том случае, когда тензор записан в каноническом виде.

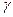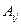Вернемся к рассмотрению симметрии тензора (1.14). Докажем, что ось Z этого тензора является осью симметрии . Матрица косинусов преобразования системы координат, отвечающего ее повороту вокруг оси Z на произвольный угол , есть матрица (1.12). Ее использование дает; все остальные равны нулю. В силу произвольности угла 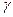можно сделать заклю­чение, что ось Z является осью симметрии для тензора (1.14). Легко проверить, что тензор (1.14) не имеет плоскости сим­метрии, перпендикулярной к оси Z, и имеет бесконечное число плоскостей симметрии, проходящих, через эту ось.

Матрица косинусов, соответствующая отражению системы: координат в некоторой плоскости, проходящей через ось Z и составляющей угол а с осью X, имеет вид

(1.15)

Используя эту матрицу, находим в соответствии с табл. 1.1 значения компонент тензора (1.14) в новой системе координат: ; , .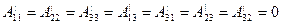

Следовательно, при таком преобразовании все компоненты тензора (1.14) преобразуются сами в себя, что показывает, что этот тензор имеет плоскость симметрии, проходящую через ось Z. Из произвольности выбора угла 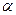следует, что таких плоскостей симметрии, проходящих через ось Z, тензор (1.14) будет иметь бесконечное множество. Можно показать, что тензор (1.14) никаких других элементов симметрии, но имеет. Набор элементов симметрии антисимметричного аксиального тензора второго ранга представляет собой , т, а группа симметрии может быть обозначена тт. Эта группа симметрии совпадает с группой сим­метрии полярного вектора, изображенного на рис.1.2,а. Значит, только на основании симметрии можно сделать вывод о том, что антисимметрич­ный аксиальный тензор определяет собой полярный вектор. Как уже указывалось, аксиальный вектор (рис.1.2,б) аналитически может быть представлен в виде антисимметричного аксиального тензора.

(1.16)

Таким образом, установление симметрии аксиального вектора сводится к установлению симметрии тензора (1.13).

Симметрия тензоров второго ранга. Для полного решения задачи о симметрии тензоров второго ранга необходимо еще рассмотреть симметрию так называемых простейших тензоров. Простейшими здесь будут называться тензоры, имеющие только одну отличную от нуля компоненту, стоящую на диагонали. Простейший полярный тензор имеет вид.

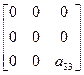(1.17)

Аналитическое рассмотрение показывает, что этот тензор имеет: ось симметрии , совпадающую с осью Z системы координат; плоскость симметрии, перпендикулярную к оси (пло­скость XY); бесконечное числа плоскостей симметрии, проходящих через ось Z; бесконечное число осей симметрии 2, перпендикуляр­ных к оси Z, и центр симметрии. Перечисленные элементы симметрии можно записать в виде , m, () m, ()2, с. Такой набор элементов симметрии совпадает с набором элементов сим­метрии цилиндра (или эллипсоида вращения), а группа симметрии тензора (1,17) может быть записана в виде .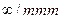

Из-за простоты рассмотрения и уже приводившихся примеров не будем доказывать существование оси и плоскостей симмет­рии т, а лишь покажем, что тензор (1.17) имеет бесконечное число осей симметрии 2, перпендикулярных к оси Z. Поворот системы координат на 180° вокруг оси, лежащей в плоскости XY и соста­вляющей произвольный угол 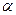с осью Y, описывается матрицей

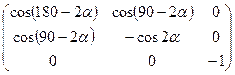. (1.18)

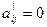Используя (1.17), получаем и все остальные , что свидетельствует о том, что взятая ось является осью симмет­рии 2. Поскольку ориентация оси в плоскости XY бралась произ­вольной, любая ось, лежащая в этой плоскости, будет осью сим­метрии 2 тензора (1.19). Простейший аксиальный тензор имеет вид

(1.19)

Элементами симметрии этого тензора являются ось симметрии , совпадающая с осью Z, и бесконечное число осей 2, перпендикулярных к оси . Из-за простоты рассмотрения доказательство сказанного опускается. Группа симметрии этого тензора обозна­чается символами 2. Именно эту симметрию имеет закрученный (скрученный) цилиндр, представляющий одну из предельных групп.

Скалярные, векторные и только что рассмотренные простейшие тензорные величины могут рассматриваться как элементарные «кирпичики», из которых можно построить любой тензор. Следует отметить при этом, что простейшие полярные тензоры могут быть как положительными, так и отрицательными. Этим двум случаям отвечают, например, растяжение и сжатие стержня. Простейшие аксиальные тензоры разных знаков соответствуют, например, закручиванию стержня по правому и левому винту. Графическое изображение простейших тензорных величин дано на рис. 1.2, в—г. Приведенные изображения правильно отражают их симметрию. Симметрия полярных тензоров второго ранга общего вида

(1.20)

и других сочетаний симметричной и антисимметричной частей полярного тензора может быть установлена, с помощью принципа суперпозиции симметрии. Так, например, суперпозиция элементов симметрии трех цилиндров разной длины, ориентированных взаимно перпендикулярно при условии, что центры цилиндров совпадают, приводит к группе симметрии ттт. Именно три плоскости симметрии, три оси вто­рого порядка и центр симметрии будут общими элементами сим­метрии для всех трех цилиндров при заданном их расположении. Этот случай соответствует симметричному тензору общего вида (1.10), которому и следует приписать группу симметрии ттт. Заметим далее, что любой полярный тензор второго ранга имеет центр симметрии. Это следует из того, что симметричный тензор даже в самом общем случае (1.10) имеет центр симметрии. Наличие центра симметрии в аксиальном векторе (антисимметричная часть полярного тензора) было показано выше. Симметрия тензора (1.9) имеет одинаковое число различающихся компонент. Легко убедиться также, что наличие «антиравных» компонент у тен­зора (1.11) не повышает его симметрию по сравнению со случаем, когда все компоненты просто различны по величине: тензор (1.11) имеет группу симметрии mтт.

Рис.1.3. Геометрическая интерпретация тензоров второго ранга общего вида: а) – полярный тензор; б) – аксиальный тензор

Таким образом, учитывая приведенные выше аргументы и зная симметрию скаляра и аксиального вектора, можно легко найти симметрию тензоров как результат суперпозиции элементов симметрии эллипсоида с эле­ментами симметрии аксиального вектора. Действительно, сим­метричная часть полярного тензора представляет собой один из эллипсоидов: шар (скаляр), эллипсоид вращения или трех­осный эллипсоид. Образно говоря, в общем случае полярный тензор может быть представлен эллипсоидом, «проткнутым» в определен­ном направлении аксиальным вектором (рис. 1.3, а). Форма этого эллипсоида и место «протыкания» определяют и сам тензор, и его симметрию.

В табл. 1.1 сведены результаты рассмотрения симметрии поляр­ных тензоров второго ранга. В таблице 1.2 приведены все различаю­щиеся по симметрии случаи в их канонической форме. Канониче­ской здесь называется форма, соответствующая записи тензора в главной системе координат его симметричной части. В этой системе координат, как известно, симметричная часть записывается только по главной диагонали тензора.

Таблица 1.2

Дата добавления: 2014-01-07