Каноническая форма и симметрия полярных тензоров второго ранга

Величина	Каноническая форма тензора	Симметрия тензора	Расположение осей
Скаляр			произвольное
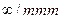
Полярный тензор			Ось совпадает с осью Z
	mmm	Ось 2 совпадает с осью X, Y, Z
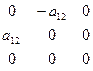
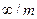
Аксиальный вектор			Ось аксиального вектора с осью Z
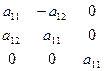
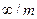
Комбинация скаляра и аксиального вектора			Ось аксиального вектора с осью Z
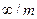
Комбинация полярного тензора и аксиального вектора			Оси полярного тензора и аксиального вектора совпадают с осью Z
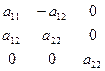
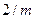
		Ось полярного тензора совпадает с осью Х
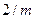
		Оси 2 полярного тензора совпадают с осями X, Y, Z
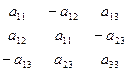
		Ось полярного тензора совпадает с осью Z
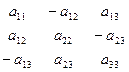
			Оси 2 полярного тензора совпадает с осью X,Y, Z

Как видно из табл.1.1, симметрия полярных тензоров второго ранга исчерпывается шестью группами. Три из них являются одновременно предельными группами симметрии. Любопытно, что число групп симметрии аксиального тензора не совпадает числом групп полярного. Это различие обусловлено тем, что аналогичные не различающимся по симметрии тензорам (1.10) и (1.11) тензоры различаются по симметрии.

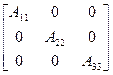; (1.21) 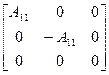(1.22)

Действительно, принцип суперпозиции симметрии в случае тензора (1.21) приводит к группе 222, в то время как для тензора (1.22) суперпозиция двух одинаковых цилиндров, имеющих «закрученность» противоположных знаков, приводит к группе 42m. В свою очередь, комбинация этой группы с полярными векторами различной ориен­тации приводит к двум группам тт2 и m — подгруппам груп­пы 42т, не имеющим аналогов среди групп симметрии полярного тензора. Кроме того, здесь не имеет аналога и одна предельная группа симметрии, получающаяся в результате суперпозиции других тензоров, имеющих оси , с полярным вектором.

Нахождение симметрии аксиальных тензоров общего вида

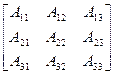(1.23)

не представляет труда и заключается в рассмотрении суперпози­ции одного из эллипсоидов, не имеющих плоскостей симметрии (шар, эллипсоид вращения, эллипсоид общего вида и т. д.), с полярным вектором. Аксиальный тензор в общем случае может быть изображен в виде эллипсоида без плоскостей симметрии, «проткнутого» полярным вектором. Форма этого эллип­соида и место «протыкания» и определяют симметрию тензора. Не все канонические формы в случае аксиального тензора имеют разную симметрию. Общее число групп симметрии аксиаль­ного тензора второго ранга оказывается равным 10.

Дата добавления: 2014-01-07