Лекция 6. Моделирование релаксационных процессов в полимерах

Выбор и описание свойств обоснованных физических моделей позволяет понять и математически описать поведение полимерных систем в различных режимах испытания. Сочетание вязких и упругих свойств одном материале, характерное для полимеров, может быть осуществлено напором и соединением в единой структуре элементов, каждый из которых обладает только упругими или только вязкими свойствами.

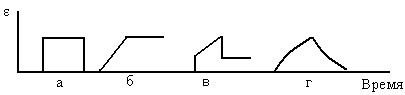
Рис. 6.1 Развитие деформации во времени при действии постоянного напряжения для моделей элементов структуры полимера: а) идеально упругая пружина; б) идеально вязкая ньютоновская жидкость (поршень, свободно перемещающийся в цилиндре); в) последовательное соединение пружины и поршня (модель Максвелла); г) параллельное соединение пружины и поршня (модель Кельвина – Фойгта)

Для характеристики поведения того или иного материала в механике принято рассматривать зависимости между прилагаемым к образцу напряжением и вызываемым им удлинением при одномерной деформации растяжения.

В качестве идеально упругого элемента такой модели можно рассмотреть стальную пружину, которая при деформации полностью подчиняется закону Гука.

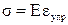
(6.1)

где Е - модуль упругости.

Упругая деформация такой пружины мгновенна и не зависит от времени, т. е. при приложении нагрузки, вызывающей в пружине напряжение σ, мгновенно возникает деформация ε, которая так же мгновенно исчезает при снятии нагрузки (рис. 6.1,а).

Идеально вязким элементом является поршень, свободно двигающийся в цилиндре с вязкой жидкостью. Его поведение подчиняется закону Ньютона, по которому в процессе деформации при приложении напряжения σ увеличивается скорость движения жидкости:

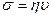
(6.2)

где 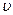– скорость деформирования вязкой жидкости, т. е

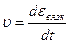
(6.3)

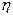– вязкость жидкости.

Деформация линейно растет со временем действия силы и не исчезает после прекращения действия силы (рис. 6.1, б), т. е. деформация полностью необратима:

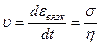
(6.4)

Очевидно, что сочетания этих двух простейших элементов могут с различной степенью точности моделировать вязкоупругие свойства полимерных тел. Наиболее простой моделью, сочетающей упругие и вязкие свойства, является предложенное Максвеллом последовательное соединение этих простейших элементов, которое проявляет эти свойства за время действия силы (рис.6.1,в). Схематически такая модель изображена на рис. 6.2

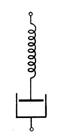
Рис. 6.2 Схема модели Максвелла

При приложении силы пружина упруго удлиняется, а поршень медленно движется. После прекращения действия силы пружина полностью восстанавливает свою прежнюю форму, а поршень остается на месте своего перемещения. Общая деформация системы (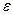) складывается из упругой (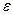_упр) и вязкой (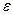_вязк) частей:

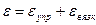
(6.5)

Дифференциальное уравнение, описывающее поведение такой системы, содержит дифференцированные, но времени уравнения законов Гука и Ньютона.

Упругая деформация в каждый момент времени определяется напряжением:

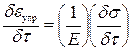
(6.6)

Согласно закону Ньютона скорость изменения деформации вязкого течения во времени постоянна:

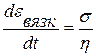
(6.7)

Тогда скорость изменения общей деформации модели по времени:

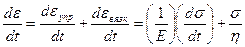
(6.8)

Релаксационные явления согласно этой модели будут проявляться как в изменении напряжения, так и деформации со временем. Если растянуть модель и затем зафиксировать достигнутую деформацию (закрепив растянутые концы модели), то скорость дальнейшего изменения деформации dε/dt = 0 и согласно уравнению (6.8).

(6.9)

После интегрирования в пределах от 0 до t и от σ₀ до σ получим

(6.10)

Следовательно, достигнутое в системе напряжение σ релаксирует от своего первоначального значения σ₀ экспоненциально как функция времени t.

Приняв

(6.11)

Получим:

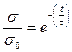
(6.12)

где τ — время релаксации системы, т. е. время, в течение которого напряжение в системе достигает 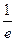первоначальной величины.

Следовательно, в полимерном материале, подвергнутом быстрой деформации, которая в дальнейшем не меняется, напряжение убывает или релаксирует с течением времени по экспоненциальному закону. Из этого видно, что время релаксации определяется отношением вязкости системы к упругому модулю ее, т.е. будет тем больше, чем больше вязкость и меньше упругий модуль.

Если на систему действует постоянное растягивающее напряжение, то согласно (6.6)

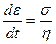
(6.13)

Это означает, что постоянное растягивающее напряжение вызывает бесконечное удлинение системы с постоянной скоростью, которая тем больше чем больше приложенное напряжение и меньше вязкость системы. Это явление называется ползучестью и проявляется в полимерном материале при действии на него постоянного растягивающего усилия. Однако упругость полимеров не идентична упругости Гука, которая связана с деформацией валентных углов и химических связей между элементами структуры. Упругость полимеров (вязкоупругость) связана с раскручиванием макромолекул при сохранении валентных углов и химических связей, т. е. с изменением формы макромолекул и взаимного расположения элементов структуры. Такое раскручивание происходит во времени, так как макромолекулы взаимодействуют друг с другом и их скольжение и раскручивание связано с преодолением сил этого взаимодействия. Следовательно, модель, отражающая это качество, должна учитывать деформацию упругого элемента в среде с определенной вязкостью. Такое запаздывание упругих свойств полимерного материала лучше отображается моделью Кельвина - Фойгта где упругий и вязкий элементы соединены параллельно (рис. 6.3).

Гонение деформации во времени (рис.6.1, г) указывает на наличие запаздывающей упругости или вязкоупругости. Поршень оказывает сопротивление установлению равновесного состояния пружины. Упругая деформация проявляется через некоторое время действия приложенной силы, которая перемещает поршень в вязкой среде.

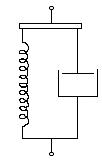
Рис. 6.3 – Схема модели Кельвина – Фойгта

Здесь можно рассматривать суммарное напряжение упругого и вязкого элементов: σ = σ_упр +σ_вяз. Но σ_упр = Еε, а σ_вяз = ηv = η(dε/dt) и σ = Еε + η(dε/dt). Если приложенное напряжение снято в момент времени t, то после интегрирования получаем:

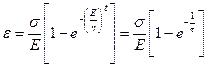
(6.14)

Здесь τ - время релаксации системы, или время запаздывания. Возвращение образца к исходной форме после удаления приложенного напряжения описывается экспоненциальной кривой:

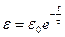
(6.15)

Модель Максвелла лучше описывает поведение линейного полимера, а модель Кельвина - Фойгта - сшитого. Обе эти модели являются качественными.

В реальных полимерах, как уже говорилось, общая деформация сочетает в себе истинно упругую деформацию Гука (модель - упругая пружина), необратимую деформацию смещения макромолекул (модель - поршень в вязкой среде) и упругую, развивающуюся во времени (высокоэластическую) вследствие раскручивания макромолекул (модель - параллельное жесткое соединение пружины и поршня). Таким образом, более точное описание свойств реального полимера может быть получено сочетанием всех этих трех элементов.

Существует несколько попыток моделировать упругие, вязкие и вязкоупругие свойства, проявляющиеся при деформировании реальных полимеров. Одной из таких моделей является модель Догадкина, Бартенева и Резниковского. Она вводит зависимость времени релаксации для описываемой полимерной системы не только от температуры и химической природы полимера, но и от величины приложенного напряжения. С увеличением последнего возрастает скорость перегруппировки сегментов макромолекул по направлению растягивающего напряжения. В процессе релаксации напряжения при постоянной деформации модели установится некоторое значение напряжения, мало меняющееся в дальнейшем, так как увеличивается энергия, необходимая для обратной перегруппировки сегментов макромолекул. Такое напряжение может быть условно принято как равновесное (σ_∞), а релаксационные процессы определяются разностью между напряжением в момент времени t и «равновесным» (σ - σ_∞). Эта модель удовлетворительно описывает поведение эластомеров (рис. 6.4).

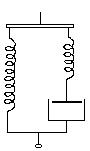
Рис. 6.4 – Схема модели Догадкина, Бартенева, и Резниковского

Вид дифференциального уравнения релаксации напряжения полимера, описываемого этой моделью, следующий:

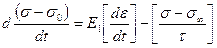
(6.16)

Однако и эта модель не дает точного количественного описания релаксационных процессов в полимере. Полнее описывает свойства аморфных полимеров еще более сложная обобщенная механическая модель полимера (рис.6.5), которая объединяет в качестве элементов последовательно соединенные модели Максвелла и Кельвина – Фойгта; при этом между упругой и вязкой частями модели Максвелла помещена модель Кельвина – Фойгта.

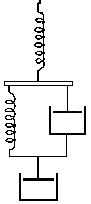
Рис. 6.5 – Схема обобщенной механической модели полимера

Изменение деформации во времени при приложении растягивающего напряжения к такой модели показано на рис. 6.6.

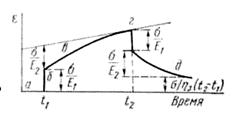
Рис. 6.6 – Развитие во времени деформации обобщенной механической модели полимера

Начальное состояние а модели длится до времени t₁, когда приложена мгновенная растягивающая сила. Она вызывает деформацию упругого элемента ε = σ/Е₁ (состояние б). Вязкоупругая деформация описывается равновесным значением деформации элемента Кельвина - Фойгта ε = σ/Е₂ и вязким течением поршня σ/η₃ (состояние в). После снятия нагрузки во время t₂ упругий элемент релаксирует мгновенно (состояние г), а вязкоупругий - медленно (состояние д). Вязкое же течение (необратимая часть деформации) остается (состояние д). Хотя эта модель и описывает главные элементы вязкоупругого поведения полимера, она тоже является упрощенной, так как вязкое течение реального полимера, имеющего широкое ММР, не является ньютоновским, а упругая часть деформации отклоняется от закона Гука.

Очень важно также, что поведение реального полимера не может описываться одним временем релаксации, а требует привлечения целого спектра (набора) времен релаксации для объяснения различных этапов деформации. Это учитывается в модели полимера, предложенной Каргиным и. Слонимским. Модель, подобная изображенной на рис.6.3, принимается ими за модель сегмента макромолекулы, а вся макромолекула представляет собой цепь последовательно соединенных сегментов (рис.6.7).

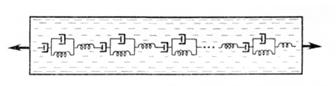
Рис. 6.7 – Модель полимера по Каргину и Слонимскому

Вязкие элементы модели движутся в общей вязкой среде, которая отражает наличие соседних макромолекул в реальном полимере. Эти макромолекулы препятствуют свободному перемещению рассматриваемой макромолекулы при деформации полимера, что и наблюдается в реальных условиях. Каждый сегмент макромолекулы обладает упругими, высоко - эластическими и вязкими свойствами, т.е. представляет собой всю только что рассмотренную обобщенную модель. Общая модель полимера Каргина и Слонимского предполагает неравномерность распределения напряжений вдоль цепей макромолекул при деформации полимеров, что имеет глубокий физический смысл для сопоставления свойств модели со свойствами реальных полимеров и позволяет исследовать закономерности деформации полимеров в связи со строением их макромолекул.

Дата добавления: 2014-01-07