Лекция 9. Равновесие трещины в упругой среде

Задачи равновесия трещины представляет значительное своеобразие в ряду других задач теории упругости. Впервые она была решена Гриффитсом в 1920 году. С точки зрения теории упругости трещина представляет собой полость в упругой среде, существующую при наличии внутренних напряжений в теле и «захлопывающуюся» при снятии нагрузки. Форма и размеры трещины существенно зависят от действующих напряжений. Поэтому математическая специфика задачи состоит в том, что граничные условия в ней задаются на поверхности, которая заранее не известна и должна сама определиться в результате решения задачи.

Рассмотрим вязкую трещину в изотропной среде, неограниченно длинную и однородную в одном направлении (вдоль оси z) и находящуюся в плоском поле напряжений 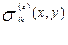; другими словами, рассмотрим плоскую задачу теории упругости. Будем считать, что напряжения симметричны относительно центра сечения трещины. Тогда профиль сечения тоже будет симметричен (рис.9.1). Обозначим его длину 2L, а переменную ширину h(x); в силу симметричности трещины

h(-x)=h(x).

y

Рис.9.1. Модель вязкой трещины в полимере

Будем считать трещину тонкой: 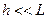. Тогда граничные условия на её поверхности можно относить к соответствующему отрезку оси x. Другими словами, трещина рассматривается как линия разрыва (в плоскости x,y), на которой испытывает скачок нормальная составляющая смещения uy =± h /2.

Введём вместо h(x) другую неизвестную функцию ψ(x), определив её как

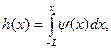ψ(-x)=-ψ(x). (9.1)

Чисто формальным образом функцию ψ(x) удобно истолковать через плотность прямолинейных (вдоль оси z), непрерывно расположенных по оси

x дислокаций, векторы Бюргерса которых параллельны оси y (полимер считается кристаллическим).Линию дислокации можно рассматривать как край поверхности разрыва, на котором смещение u испытывает скачок b. В представлении (9.1) скачок h нормального смещения в точке x рассматривается как сумма векторов Бюргерса всех дислокаций, проходящих левее этой точки (равенство же означает, что дислокации справа и слева от точки x =0 имеют разный знак).

Такое представление позволяет сразу написать выражение для нормальных напряжений (σyy) на оси x. Они складываются из напряжений σyy (x,0), приходящих от внешних нагрузок (обозначим их для краткости 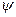(x) и напряжений σyy (x), создаваемых деформацией от трещины. Рассмотрим последние как создаваемые распределёнными на отрезке (-L,L) дислокациями, получим:

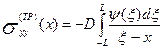(9.2)

( для точек на самом отрезке (-L,L) интеграл должен пониматься в смысле главного значения). Для изотропной среды

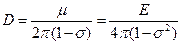(9.3)

Напряжения же σxy, создаваемые такими дислокациями в изотропной среде, обращаются на оси x в нуль.

Граничное условие на свободной поверхности трещины, отнесённое (как указывалось выше) к соответствующему отрезку оси x, требует обращения в нуль нормальных напряжений σyy = σyy + p(x). Это условие, однако, должно быть уточнено в связи со следующим обстоятельством.

Сделаем предположение (которое подтвердиться получающимся результатом), что на краю трещины её берега смыкаются плавным образом, так что вблизи края обе поверхности сближаются до очень близких расстояний. В этих условиях необходимо учитывать силы молекулярного притяжения между поверхностями, действие которых распространяется, как известно, на расстоянии r0, большие по сравнению с межатомными. Эти силы будут играть существенную роль в узком участке вблизи края трещины, в котором h ≤ r0 (обозначим порядок величины длины для этого участка через d; его оценка будет дана ниже).

Пусть G есть сила молекулярного сцепления, отнесённая к единице площади трещины; она зависит от расстояния h между поверхностями. С учётом этих сил граничное условие напишется в виде:

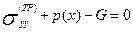(9.4)

Естественно предположить, что форма трещины на участке вблизи её края определяется характером сил сцепления и не зависит от приложенных к телу внешних нагрузок. Тогда при определении формы основной части трещины по внешним силам p(x) величина G приобретает характер не зависящей от p(x) заданной функции G(x) (на участке d, где она только и существенна). Подставив в (9.4) σyy из (9.2), получим, таким образом, следующее интегральное уравнение для ψ(x):

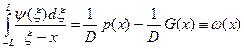(9.5)

Поскольку края трещины предполагаются не закреплёнными, напряжения на них должны оставаться конечными. При нашем выборе начала координат (в середине отрезка (-L,L)) эта формула имеет вид

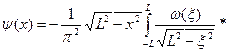
. (9.6)

При этом должно выполняться условие, согласно которому в данном случае

(9.7)

(воспользовавшись симметрией задачи, мы перешли от интеграла по отрезку (-L,L) к интегралам от 0 до L). Поскольку G(x) отлично от нуля лишь в области L – x ~ d, то во втором интеграле можно положить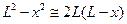, и тогда условие (9.7) принимает вид

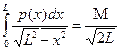(9.8)

где через M мы обозначили константу (зависящую от материала среды):

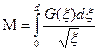(9.9)

Эта константа может быть выражена через обычные макроскопические характеристики тела - его упругие модули и поверхностное натяжение α;

как мы увидим ниже, эта связь даётся формулой:

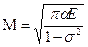(9.10)

Равенство (9.8) представляет собой уравнение, определяющее длину трещины 2L по заданному распределению напряжений p(x). Так, для трещины, растягиваемой сосредоточенными силами f, приложенными к середине её сторон (p(x) = f σ(x)), находим:

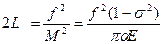(9.11)

Следует, однако, иметь в виду, что устойчивое равновесие трещины возможно не при всяком распределении p(x). Так для однородных растягивающих напряжений (p(x) = const ≡p0) получим:

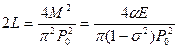(9.12)

Для геометрической модели трещины в виде двойного сектора, образованного пересечением двух окружностей радиуса-r, (метод «набухающих окружностей») величина напряжения будет 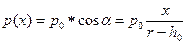, 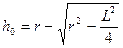. Учитывая L << r получаем для радиусов моделирующих окружностей ~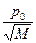, т.е. размер трещины растет пропорционально приложенному напряжению.

Дата добавления: 2014-01-07