XIII.- законы склеивания

XII.- законы поглоще­ния.

Для сокращения и лучшей обозримости записей бу­дем иногда опускать знак конъюнкции (так же как опус­кают знак умножения), условившись под выражением ХY подразумевать формулу (X /\ Y). Так, например, вме­сто формулы (X /\ У)\/Z будем иногда писать ХУ\/Z ‑ запись X(Y\/Z)X нужно понимать как формулу (Х /\(Y/\Z))\/.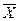

Обратим внимание на характер соответствий между равносильностями, объединенными в пары под номерами V-XIII. В этих соответствиях проявляется так назы­ваемый принцип двойственности.

Две фор­мулы, не содержащие знаков → и ↔, называются двой­ственными, если каждую из ник можно получить из другой заменой /\, \/, и, л соответственно на \/, /\, л, и.

Принцип двойственности утверждает следующее: если две формулы (не содержащие знаков → и ↔) равно­сильны, то двойственные им формулы тоже равносильны.

Например, для формулы л двойственной является формула и, а для формулы Х/\л — формула Х\/и; убе­дившись, что Х/\л≡л, согласно принципу двойственности получаем равносильность Х\/и≡и.

4. Выражение импликации и эквиваленции через конъюнкцию, дизъюнкцию и отрицание. До сих пор мы занимались равносильными преобразованиями формул, не содержащих знаков → и ↔. Сейчас покажем, что всякую формулу, содержащую → или ↔ можно заменить
равносильной ей формулой, не содержащей этих знаков.

Имеют место следующие равносильности (проверь­те!):

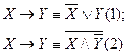
Будем говорить, что равносильность (1) выражает им­пликацию через дизъюнкцию и отрицание, а равносиль­ность (2) — через конъюнкцию и отрицание.

Эквиваленция выражается через конъюнкцию и импликацию равносильностью

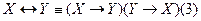
(проверьте!). Из равносильностей (3) и (1) получаем равносильность

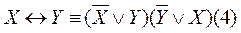
выражающую эквиваленцию через конъюнкцию, дизъюнкцию и отрицание. Из равносильностей (3) и (2) получаем равносильность

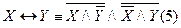
выражающую эквиваленцию через конъюнкцию и отри­цание.

Очевидно, что в принципе можно было бы обойтись всего двумя операциями: конъюнкцией и отрицанием.

Возникает вопрос: а нельзя ли выразить через какую-ни­будь одну операцию все остальные? Можно доказать, что ни через одну из введенных здесь пяти логических операций этого сделать нельзя. Нужны, по меньшей мере, две операции; при этом одной из них обязательно должно быть отрицание.

Все остальные операции можно выра­зить через конъюнкцию и отрицание, дизъюнкцию и от­рицание или импликацию и отрицание. Через эквиваленцию и отрицание остальные операции выразить нельзя.

Зачем же вводить пять операций, когда можно обой­тись двумя? Напомним, что введенные пять операций соответствуют наиболее употребительным союзам. Ис­пользование лишь двух операций усложнило бы формализацию предложений естественного языка и привело 6ы к громоздким, труднообозримым формулам. В других приложениях математической логики эти доводы в пользу введения и употребления всех пяти операций теряют силу; там ограничиваются меньшим числом опера­ций. Аналогичное положение имеет место в арифметике: всякое число может быть записано с помощью двух цифр: 0 и 1; однако, поскольку записи чисел и выкладок в двоичной системе счисления очень громоздки, мы при­бегаем к этой системе лишь в специальных случаях.

Можно ввести логическую операцию, через которую выражаются все пять операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция. Такова, напри­мер, операция, соответствующая сложному союзу «не A или не B» («или» — неразделительное). Эта операция обозначается символом | (например, А|В) и получила название штрих Шеффера. Штрих Шеффера определяет­ся с помощью такой таблицы:

X	Y	Х|Y
и	и	л
и	л	и
л	и	и
л	л	и

Непосредственно из таблицы видно, что Х|У≡.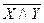

Легко убедиться (сделайте это!), что Х|Х≡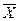. Из этих двух равносильностей следует, что X/\Y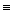(X|Y)|(X|Y).

Таким образом, нам удалось выразить через штрих Шеффера отрицание и конъюнкцию, а через них, в свою очередь, можно выразить дизъюнкцию, импликацию и эквиваленцию.

Дата добавления: 2014-01-07