Лекция № 5 ВА-1, матан, 2 семестр

Тема. Задача, приводящая к понятию определенного интеграла. Определение понятия определенного интеграла, классы интегрируемых функций. Основные свойства определенного интеграла. Формула Ньютона-Лейбница.

Существует ряд задач, для решения которых необходимо применение определенного интеграла. Одной из таких задач, возникших в глубокой древности, является задача определения площади плоской фигуры, ограниченной линией произвольной формы. С нее мы и начнем.

1 Задача, приводящая к понятию
определенного интеграла.
Понятия определенного интеграла

Задача 1.1. Определить площадь фигуры 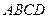(рис. 1.1), ограниченной линиям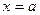и , , и . Фигура 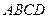носит название криволинейной трапеции.

Эта задача не может быть решена методами элементарной математики, поскольку в элементарной математике возможно вычисление площадей фигур, ограниченных отрезками прямых и дугами окружностей (многоугольники, окружность и ее части и т.д.). Рассмотрим иной подход к решению этой задачи.

Имеем фигуру, ограниченную осью OX, прямыми , 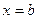и кривой (рис. 1.1). Эта фигура называется криволинейной трапецией.

Разделим отрезок произвольным образом на малые отрезки (они называются элементарными отрезками) точками:

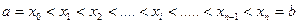(1.1)

и через точки деления проведем прямые, параллельные оси .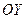

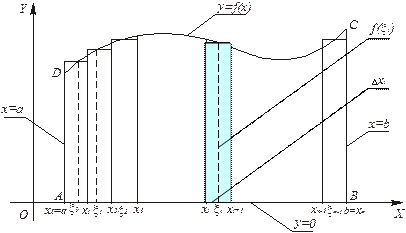Рис. 1.1

В результате криволинейная трапеция 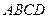разобьется на элементарные полоски. Заменим каждую полоску прямоугольником с основанием, совпадающим с основанием полоски , и с высотой, равной ординате – функции 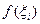произвольной точки основания . Площади прямоугольников выразим формулой:

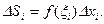(1.2)

Просуммируем площади всех прямоугольников, получим величину , приближенно равную площади криволинейной трапеции:

(1.3)

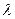Сумма (1.3) называется интегральной суммой для функции на отрезке . Обозначим через наибольший из отрезков и устремим 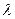к нулю. Тогда будут стремиться к нулю и длины всех отрезков , что означает переход от одного разбиения к другому на все более мелкие элементарные отрезки. При этом ступенчатая фигура, заменяющая криволинейную трапецию, все более будет приближаться к криволинейной трапеции. Вместе с этим, будет изменяться и сумма . Если при этом величина стремится к конечному пределу 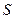, не зависящему от способа разбиения на элементарные отрезки и выбора на каждом из них точки 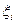, то эта величина 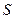и принимается за площадь криволинейной трапеции :

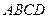. (1.4)

Дата добавления: 2014-01-07