Общее уравнение прямой

Лекция № 7, АС12-14, анге, 2 сем, 2013

Тема. Общее уравнение прямой. Различные виды уравнения прямой. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых.

Запишем уравнение прямой с угловым коэффициентом в виде:

.

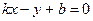Угловой коэффициент k может иметь любые значения. Если, например, k – обыкновенная дробь, то после преобразований получим уравнение, в котором коэффициент при 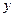не равен единице. Поэтому в общем случае уравнение запишем в виде:

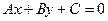. (1.1)

Уравнение (1.1) носит название общего уравнения прямой, коэффициенты А и В в нем не могут быть равны нулю одновременно.

2. Уравнение прямой, проходящей через
данную точку в заданном направлении.
Уравнение пучка прямых

Поставим задачу. Составить уравнение прямой, проходящей через точку 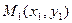и образующей с осью OX угол .

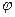Решение. Потребуем, чтобы выполнялось условие 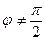и воспользуемся уравнением прямой линии с угловым коэффициентом:

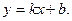
Подставим в это уравнение координаты точки :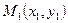

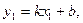
найдем из него величину 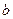, 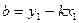и подставим ее в уравнение с угловым коэффициентом:

.

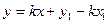После преобразований последнее уравнение примет вид:

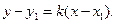(2.1)

Уравнение (2.1) – это искомое уравнение прямой 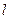, проходящей через точку 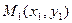и образующей с осью OX угол 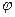(рис 2.1).

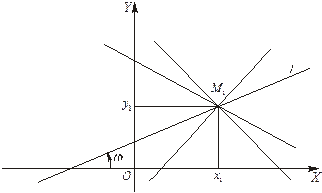Рис. 2.1

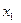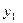Если в уравнении (2.1) зафиксировать координаты и точки 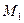, а величие 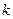придавать различные значения, то уравнение (2.1) будет представлять совокупность прямых, проходящих через точку 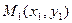, за исключением прямой, параллельной оси OY. Эта совокупность называется пучком прямых с центром в точке 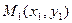(рис. 2.1). В случае, когда 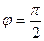, уравнение прямой, проходящей через точку 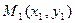, имеет вид:

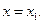
Задача 2.1. Составить уравнение прямой, проходящей через точку 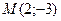и образующей с осью OX угол .

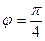Решение. Найдем 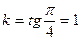. Эту величину 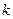и координаты точки М подставим в уравнение (2.1), получим:

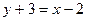
отсюда

.

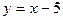3. Уравнение прямой, проходящей через две
заданные точки

Рассмотрим задачу: Даны две различные точк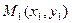и: и 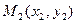. Составить уравнение прямой, проходящей через эти точки (рис.3.1).

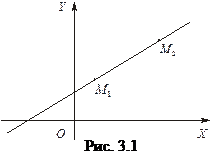Решение. Воспользуемся уравнением пучка прямых (2.1), проходящих через точку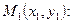

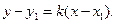(3.1)

Выделим из пучка прямую, проходящую через точку 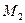. Для этого подставим в уравнение пучка координаты точки 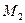, получим:

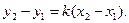
Из последнего уравнения определяем величину k:

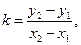
которую подставляем в уравнение (3.1):

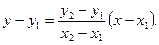(3.2)

После преобразований уравнение (3.2) примет вид:

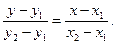(3.3)

Уравнение (3.3) – искомое уравнение прямой, проходящей через две заданные точк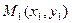и и .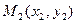

В уравнении (3.3) один из знаменателей может оказаться равным нулю (оба одновременно равняться нулю они не могут, так как точки различны).

Если 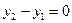, то прямая параллельна оси 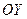и ее уравнение имеет вид:

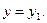
Если 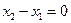, то прямая параллельна оси и ее уравнение имеет вид:

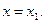
Задача 3.1. Составить уравнение прямой, проходящей через точк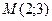и и .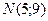

Решение. Для решения задачи следует воспользоваться уравнением (3.3). При этом безразлично, какую из точек считать первой, а какую – второй. Покажем это, считая вначале первой точку М, а затем точку N.

, , ,

, , ,

.

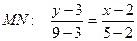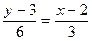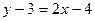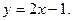
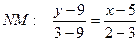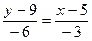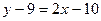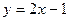Результаты совпали.

Дата добавления: 2014-01-07